UCR Department of Computer Science & Engineering

CS177 Notes on Q-Q Plots

Mart Molle, February 2008

I. Background

Q-Q plots are discussed on pages 334-338 in the textbook by A. M. Law (Simulation Modeling & Analysis, 4th Ed), under the subheading Probability Plots. The discussion focuses on using the technique to compare the cumulative PDFs for two (assumed to be continuous) random variables, where: Q-Q plots are one of several heuristics for testing "goodness of fit" between a theoretical distribution and some empirical data, i.e., how reasonable is it to assume that the empirical data set was generated by sampling the chosen theoretical distribution? The principal advantage of Q-Q plots over other heuristics is that a "good fit" is easy to recognize. This is because the technique reduces the two separate cumulative distribution functions for X and Y into a simple curve on the X-Y plane:
Although the discussion in the textbook [near bottom of p. 336] assumes the cumulative distribution function is invertible (in which case the random variable must be continuous), it seems clear that Q-Q plots can be used whether or not we assume that the distribution of Y is continuous. (Note, in particular, that the PDF for X is always discrete, because it is based on a finite number of measurements.) For consider the following "thought experiment'' by which we might construct the true PDF for some random variable as the limiting case of an empirical
distribution. That is, we sample the r.v. N times and then sort the samples into non-decreasing order. Now in the limit as N grows very large:
Thus, for any r.v. X, discrete or continuous, we can find the qth quantile of its distribution as that value xq which is the minimum in the set {x | F (x) > q}. In other words:
Operationally, this last statement shows that we would be better off describing a random variable by its inverse PDFs -- even though convention dictates the opposite! This change in perspective would have no significant impact on continuous random variables, since the two graphs, showing FX(x) as a function of x and FX-1(q) as a function of q, are identical except for "flipping" the image along its main diagonal. On the other hand, if we apply the same "flipping" to the inverse PDF for a discrete random variable, then the resulting "staircase-like" graph of FX(x) as a function of x would include the vertical face of each "step" but not the horizontal "tread". The advantage of this change in perspective is clear in this application:
Thus, in terms of the inverse PDFs, a Q-Q plot for the random variables X and Y may be defined as the locus of points on the X-Y plane of the form:
(FX-1(q),  FY-1(q))     for all q between 0 and 1.

Notice that the independent variable, q, doesn't actually appear the graph! Moreover, if one of these functions, FY-1(q) say, happens to be invertible, then the definition of the Q-Q plot can be simplified by eliminating the quantile variable q from the above expression to give:
(x,  FY-1(FX(x)))     for all x over the domain of X.

In this case, the following Turing procedure could be used to generate the Q-Q plot, assuming the empirical data (sorted into non-decreasing order) are stored as the first n elements as the array Data, and the function inversePDF can be invoked to evaluate FY-1(q):

procedure continuous_Q_Q (Data : array 1 .. * of real, n : int, function inversePDF (x : real) : real)
for i : 1 .. n
put Data (i), " ", inversePDF ((i - 0.5) / n) % See text, bottom of p. 334
end for
end continuous_Q_Q

II. An Example where the Theoretical Distribution is Assumed to be Continuous

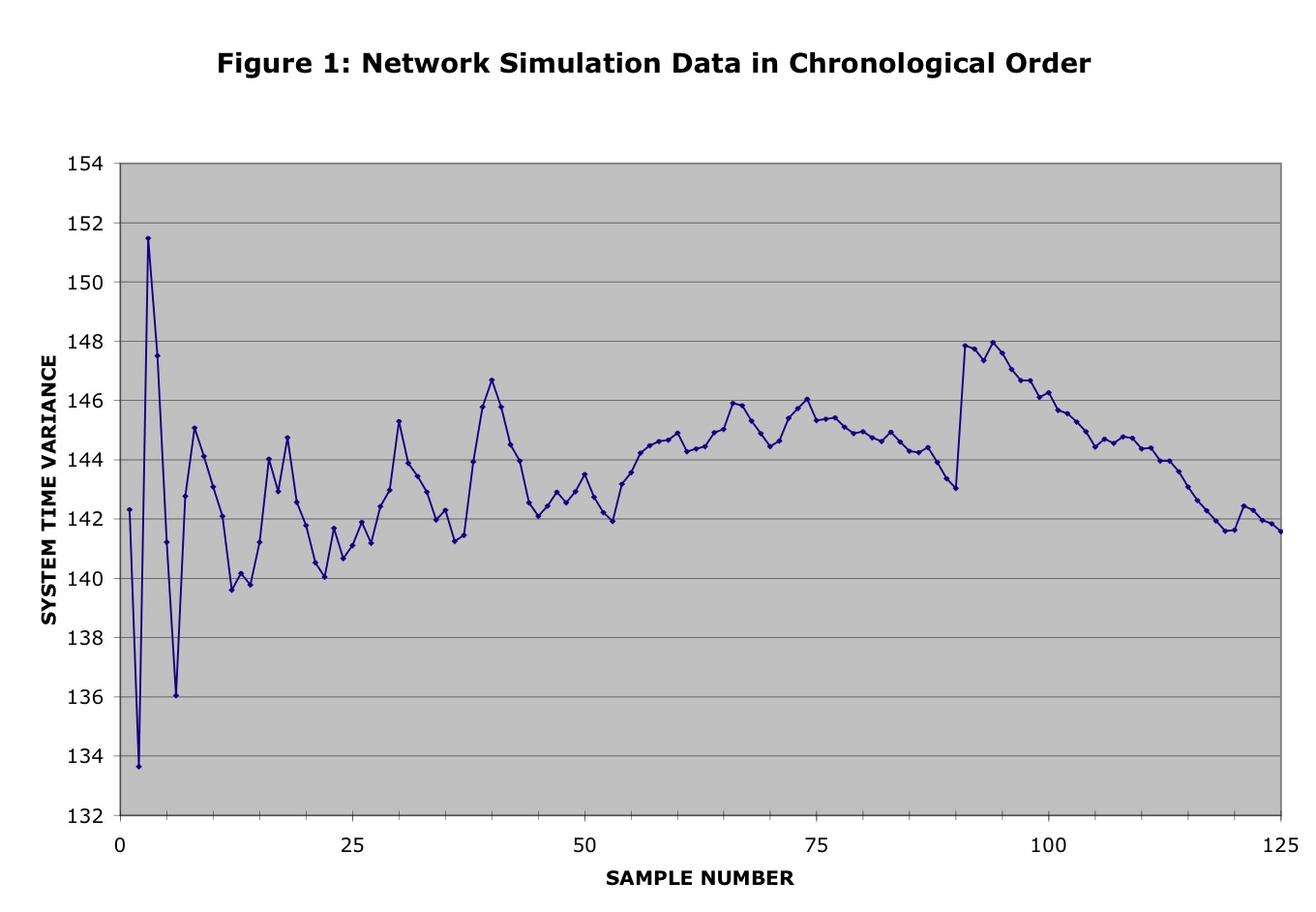
An application of this procedure is shown in Figures 1-4. Figures 1-2 contain some empirical data collected from a very long simulation of a novel token ring local area network. This particular run was divided into 125 batches, each containing the statistics for 91,431 packets. (Thus, more than 11.4 million packets were delivered during the simulation).

Figure 1 shows a graph of sample variance versus time for the raw data file, where the x-coordinate of each point is the batch number in chronological order and the y-coordinate is the sample variance for the packets contained in the corresponding batch.

Figure 1: Original data from a continuous distribution
Figure 1: Original data present in chronological order

Similarly, Figure 2 shows corresponding graph for the sorted data file, where the same set of empirical data has been sorted into non-decreasing order according to the sample variance to yield an inverse PDF function:
FX-1(k/125)    for all 1 < k < 125.
Figure 2: Data sorted into non-decreasing order
Figure 2: The same data sorted into non-decreasing order

Thus, the question now is to try to "fit'' some theoretical distribution to this data. Since each of the points is a batch statistic (and the batch size is quite large), we expect the Central Limit Theorem to apply, and hence that the data should have a normal distribution. Figure 3 gives a Q-Q plot of the empirical data on the x-axis versus a standard normal distribution on the y-axis. (We dropped the first 10 samples from the raw data, because they do not seem to be representative of the steady-state behaviour of the system.)

Figure 3: Q-Q Plot of empirical vs. normal distribution
Figure 3: Q-Q Plot of empirical data vs. Standard  Normal distribution

Observe that the QQ Plot is quite straight, and closely follows the (dashed) linear trend line, but that it doesn't pass through the origin, nor does it have a slope of 45 degrees. Thus, we can conclude that a normal distribution is a good fit to the data -- provided we select the appropriate values for the mean and variance.

For comparison, Figure 4 gives the corresponding Q-Q plot when we change the theoretical distribution from the Standard Normal distribution to the exponential distribution with rate unity. This time the QQ Plot is obviously very different from the (dashed) linear trend line, so it is easy to see that the exponential distribution is not a good fit to the data.

Figure 4: Q-Q Plot of empirical vs. exponential distribution

Figure 4: Q-Q Plot of empirical vs. exponential distribution

III. Generation of Q-Q Plots from Two Discrete Distributions

The situation is a bit more complicated when the theoretical distribution is assumed to be discrete. For example, consider the following pedestrian count data that was collected by my CS177 class in 2003.  Over a particular one-week period, each student spent some time counting the number of pedestrians traveling back and forth between remote parking lot 30 and the UCR main campus at various 5-minute periods. Clearly, the number of pedestrians passing the observation point during some observation period must be a non-negative integer. Therefore, we should choose a theoretical distribution that is also non-negative and integer-valued. In this case, the obvious choice is the Poisson distribution, which is commonly used to represent the number of events that occur in a fixed-length interval, assuming that the events occur independently at some constant rate.

We are now ready to describe the generation of a Q-Q Plot, assuming that the empirical random variable X is given by a tabulated discrete n-element distribution:

{X(i) : i = 1, ..., n}with respective cumulative probabilities FX(X(i)) = (i - 0.5) / n,

and the theoretical random variable Y has a discrete distribution FY(y), in which Y can take only only m distinct values:

{yj : j = 1, ..., m} with respective individual probabilities pj and cumulative probabilities FY(yj).

Without worrying about program efficiency, we could generate the Q-Q Plot simply letting q increase from 0 to 1 in infinitessimally small steps, and for each chosen value of q, we add the point (X(i), yj) to the graph, where:
Unfortunately, however, the same point (X(i), yj) gets added to the graph many times, since the inverse PDFs are piecewise constant over a range of q values. For example, the point (X(1), y1) is chose for every value of q between 0 and min {0.5 / n, p1}. Conversely, it is easy to see that the algorithm can never generate more than n+m distinct points. To see this, we observe that the x-coordinate of the intersection point between the horizontal line y = q and a "staircase-like" discrete cumulative distribution function F(x) only changes as q hits the top of each of its "steps". Therefore, to speed up the algorithm and avoid generating all those duplicate points, we will construct an "event driven simulation" of a program that increases q continuously. In this case, the value of q jumps directly from the top of one "step" to the next, where it generates a single copy of the point (FX-1(q),  FY-1(q)). Here is an implementation of this technique, in the form of a Turing subprogram:

procedure integer_Q_Q_Plot (sortedData : array 1 .. * of int, n : int, PDF : array 1 .. * of record
value : int
cumulative_prob : real
end record)

% Perform an "event driven simulation" of the result of trying to construct a q-q plot of two integer valued PDFs
% by letting q increase smoothly from 0 to 1 and then listing the sequence of (Y, X) pairs that are generated
% by the intersections of the two PDFs with the line Y=q.

const TOL := 0.95 % magic constant, keeps us out of trouble if the theoretical distribution has a long tail

var j : int := 1  % index across possible values for the theoretical distribution
var Y : int := PDF (j) .value % theoretical Y, non-negative integer valued
var Yq := PDF (j).cumulative_prob % next critical quantile for Y

% Now Y = the min value for which the r. v. has some mass, and Yq = the corresponding cutoff point for the PDF

var X : int := sortedData (1) % empirical X, non-negative integer valued
var Xq := 1 % n times the next critical quantile for X
loop
exit when Xq = n or sortedData (Xq + 1) not= X
Xq += 1
end loop

% Similarly, X = the min value for which the empirical data has some mass, and Xq / n is the corresponding cutoff point

loop
put Y, " ", X
exit when Xq = n and (Yq > TOL or j = upper (PDF))
if Xq / n < Yq then % X crosses a critical quantile first, so advance to the next cutoff point
loop
Xq += 1
exit when Xq = n or sortedData (Xq + 1) not= sortedData (Xq)
end loop
X := sortedData (Xq)
elsif Yq < Xq / n then % Y crosses a critical quantile first, so advance to its next value
j += 1
Y := PDF (j) .value
Yq := PDF (j).cumulative_prob
else % both hit a critical quantile together
loop
Xq += 1
exit when Xq = n or sortedData (Xq + 1) not= sortedData (Xq)
end loop
X := sortedData (Xq)
j += 1
Y := PDF (j) .value
Yq := PDF (j).cumulative_prob
end if
end loop
end integer_Q_Q_Plot

Let us now return to the pedestrian count example introduced at the beginning of this section. The raw data collected by students is available on sheet 1 of this Excel spreadsheet, while figure 5 plots the number of pedestrians travelling towards campus per 5-minute interval as as a function of time-of-day. The data in this figure is rather messy and shows a high degree of non-stationarity in terms of both a general downward trend (i.e., most students come to campus in the morning) and periodicity (i.e., the counts tend to increase significantly at the boundary between class timeslots, which happen on the hour on Monday-Wednesday-Friday, and once every 90 minutes on Tuesday-Thursday).

Jagged Lines, decaying towards the afternoon
Figure 5: 5-Minute Pedestrian Counts as a Function of Time-of-Day

Notice that the pedestrian count data collected between 1pm and 4pm seems relatively stable, so we shall limit our attention to this "afternoon data" subset of the raw data. After reviewing a sorted copy of the afternoon data (found on sheet 2 of the spreadsheet), it is evident that one point (38 pedestrians, collected at 1:55pm on Wednesday -- and hence just ahead of a class timeslot) should be discarded becuase it is so different from the other 37 samples -- where the pedestrian count distribution has average is 11.7 and maximum of 28.  Figure 6 shows a discrete Q-Q Plot comparing the afternoon data to a Poisson distribution with mean 11.7. Notice that the graph is a set of disconnected points and not a continuous curve, since neither random variable can ever take on any non-integral values. However, the points are surprisingly-well clustered along the linear trend line, considering the messiness of the data.

Q-Q Plot closely follows a linear trend line
Figure 6: Discrete Q-Q Plot of Fitting a Poisson Distribution to the Pedestrian Counts

At first glance, the linearity of figure 6 seems to validate our choice of Poisson for the theoretical distribution: a straight line indicates that the empirical and theoretical distributions belong to the same "family", i.e., they have the same shape but might have different values for a location parameter (if the line does not pass through the origin) and/or a scale parameter (if the slope of the line is not 45 degrees). However, even though we set the mean of the Poisson distribution to the mean pedestrian count, neither the y-intercept nor the slope of the line matches the "ideal" value so this Poisson distribution is not a perfect match. Unfortunately, the Poisson distribution has only one adjustable parameter (its mean), making it impossible to force the Q-Q Plot to become a 45 degree straight line through the origin. Therefore, we must ultimately reject the Poisson distribution for modeling the "afternoon data". The reason for this failure can be seen from a comparison of the two cumulative distribution functions, as shown in figure 7.

Two PDFs with significantly different slopes.

Figure 7: Cumulative Distributions for "afternoon data" and Poisson with Same Mean.

The empirical PDF for the empirical PDF for the afternoon data rises much more gradually than the PDF for the Poisson distribution with the same mean. This is because the variance of the "afternoon data" is significantly higher than the variance of the Poisson distribution. Since the mean and variance are always equal for the Poisson distribution, this discrepancy can only be fixed by choosing a different theoretical distribution.