CS 30 Notes on Using Matrix Operations
to Model the Flow of Materials in a Refinery
Mart Molle, April 2011
Background
This material is based on my experience as an undergraduate student
intern during the summer of 1975, doing computer programming to support
the engineers managing a copper refinery in northern Canada. I have
forgotten plenty of details, and simplified many others to make the
example easier to understand. Please don't
try to construct a smelter
based on these instructions! For the purposes of this example,
let's assume that refining copper ore into finished copper bars
requires two
processing steps, as shown in the following flow diagram.
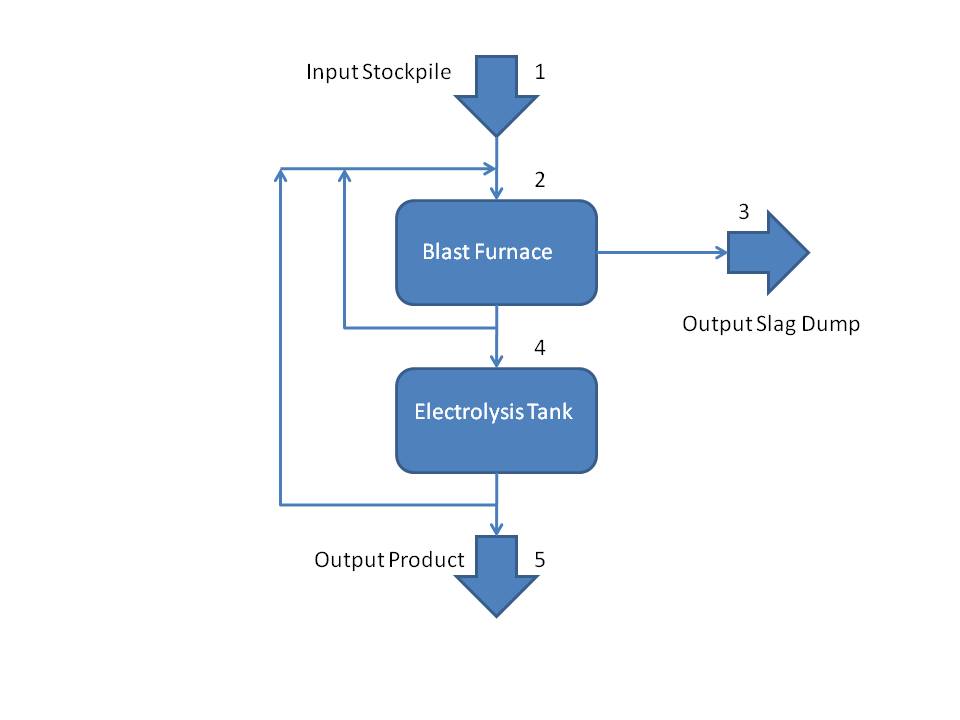
The smelting process begins by loading some raw materials (copper ore
mixed with other inputs, such
as silica and coal) into a blast
furnace. Then lots of heast is applied until the mixture melts
and then separates into several
layers -- just like oil and water in a bottle of salad dressing, or the
fat and meat juices you collect from the bottom of the roasting pan
when making gravy. In this case, the top layer is impurities suspended
in molten silica, called slag,
which
cools into a solid material that looks like lava and is discarded
as waste. The bottom layer is rough copper, which is cast into slabs in
preparation for the second step. In between is an undifferentiated
mixture of ingredients with similar composition to the raw materials.
For the purpose of this example, let's assume that one "batch" of raw
materials at a time is processed by the blast furnace:
- The input is 100 tons total weight of raw materials
(approximately 10% copper and 90% other);
- The outputs, at the
end of an 8-hour shift, consist of:
- 40
tons of slag (0% copper, 100% other),
- 10 tons of rough copper
(75% copper, 25% other), and
- 50 tons of leftover material (5% copper,
95% other).
In addition, let's assume that the refining process carried out by the
furnace distributes the input copper among the three outputs
independently of all other material present inside the smelter. In
other words, looking only at the
processing of copper in our example, we see:
- The input is raw material that contains 10 tons of copper (100
tons * 10%)
- The outputs consist of:
- slag that contains 0 tons of copper (40 tons * 0%)
- rough copper that contains 7.5 tons of copper (10 tons * 75%)
- leftover material that contains 2.5 tons of copper (50 tons *
5%)
The second step of the smelting process
involves electro-deposition, which is similar charging a battery or
applying chrome plating to the exhaust pipes of a motorcycle. In this
case, the rough copper bars are immersed in a tank of electrolyte next
to some sheets of refined copper. When a DC voltage is applied between
the anode (rough copper) and cathode (refined copper), the copper atoms
move through the electrolyte as charged ions from anode to cathode,
until the anode is reduced to some left-over sludge (containing 10% copper, 90%
other) sitting on the bottom of the tank and the cathode has
grown into a large piece of refined
copper (containing 99% copper, 1% other).
Note, that
this information only tells us the relative amount
of copper in each output product, without giving you the total weight
of each output the way we had for the blast furnace. However, we can
find this missing incredient by solving a "mass
balance" equation for tracking the movement of copper. Assuming that no
material is created or destroyed inside the electolysis tank, our input
of 10 tons of raw
copper must generate a total of 10 tons of output, which is
split into z
and (10 - z)
tons,
respectively, of sludge
and refined copper.
Similarly,
the
total
amount
of
copper
(in
tons) entering and leaving the electrolysis tank is also equal, which
gives us the
following equation for the movement of copper:
10 * 0.75 = z * 0.1 +
(10 - z) * 0.99
This equation can be easily solved algebraically to give
z = 2.4 / 0.89 = 2.697
(Remember that the above lines are equations, not Matlab
commands, and the first line in particular will generate a Matlab
error, rather than doing what you wanted!)
Therefore, once we have found z, we can
represent the processing of copper at the electrolysis tank as follows:
- Input is rough copper that contains 7.5 tons of copper (10 tons *
0.75)
- Outputs consist of:
- sludge that contains 0.27 tons of copper (z tons of sludge
* 10%)
- refined copper that contains 7.23 tons of copper ((10 - z) tons of
refined copper *
99%)
In other words, the processing in the
electrolysis step distributes the input copper so that
(0.27 tons) / (7.5 tons) = 3.6%
is caught in the sludge, and the remaining
(7.23 tons) / (7.5 tons) = 96.4%
leaves the smelter in the form of its primary product: refined
copper bars.
It is also very important to not to forget about the
sludge, which is an "unwanted" output product generated by the
electrolysis tank. Since
the sludge the same concentration of copper (10%) as the original raw
materials entering the smelter, the sludge must be returned to the
blast furnace for further processing, rather
than simply thrown away.
Modeling the Smelter with Matlab
After a few preliminary calculations (i.e., solving for z), we have
converted the operation of the smelter into a series of simple
formulas, to say how the amount of copper (say) in each input/output
stream or processing step depends on the others. Thus, we could easily
write down a series of Matlab assignment statements to show how these
values change from one shift to the next. For example, suppose the
smelter is initially idle after a long vacation, and the first shift
shows up for work and starts to bring the smelter back online. Since
both the blast furnance and electrolysis tank are empty, the only crew
members at the input stockpile can do any real work, namely moving 10
tons of raw materials to the entrance of the blast furnace. Thus, a
"snapshot" of the smelter taken during the first shift can be
summarized by the following Matlab statement:
% first shift
input_copper = 10;
%
prepare
first
batch
of
raw
material
Similarly a smelter "snapshot" during the second shift looks like this.
The blast furnace crew has loaded the
input copper into the furnace and is now heating it. The
stockpile crew is moving another 10 tons of raw materials to the
entrance
of the blast furnace. All other crew members are still idle, so the new
"state" of the smelter looks like this:
% second shift
blast_furnace =
input_copper;
%
load
blast
furnace
input_copper
= 10;
%
prepare
another batch of raw
material
As the process continues, we get the follow sequence of Matlab
statements:
% third shift
slag =
blast_furnace * 0.0; % empty the blast furnace
raw_copper =
blast_furnace * 0.75;
leftovers = blast
furnace * 0.25;
blast_furnace =
leftovers + input_copper; % reload the blast furnace
input_copper =
10; % prepare another back of raw material
tank = raw_copper;
%
load
the
electrolysis
tank
slag_dump = slag;
%
disposal
crew
takes
slag
to dump
slag
=
0;
% fourth shift
slag =
blast_furnace * 0.0; % empty the blast furnace
raw_copper =
blast_furnace * 0.75;
leftovers = blast
furnace * 0.25;
sludge =
raw_copper * 0.036; % empty the electrolysis
tank
refined_copper =
tank * 0.964;
tank = raw_copper;
%
reload
the
electrolysis
tank
blast_furnace =
leftovers + input_copper + sludge; % reload the blast furnace
input_copper =
10; % prepare another back of raw material
output_product =
refined_copper;
% shipping crew sends final product to market
refined_copper
=
0
slag_dump = slag;
%
disposal
crew
takes
slag
to dump
slag
= 0;
% fifth shift ... Looks exactly the same as the fourth shift
Simplifying the Model by Introducing Matlab Matrix/Vector Notation.
Vector notation allows us to combine the results of one processing
"step" at the blast furnace, i.e.,
slag = blast_furnace *
0.0; % empty the blast furnace
raw_copper =
blast_furnace * 0.75;
leftovers = blast
furnace * 0.25;
into a single Matlab command:
blast_out
=
blast_furnace
*
[0.0
0.75
0.25]
blast_out
=
0 7.5000 2.5000
(where I have shown the answer produced by Matlab in red to
separate it from the commands I've been typing). The only
"inconvenience" is that I must recognize each output product by its
position in the vector, rather than a "nice" individually-chosen
variable. Don't worry, things will make more sense in a moment!
Notice that all the objects in the smelter diagram has been numbered
from 1 to 5. Therefore, let's begin by using those numbers to identify
each smelter object by its position in a 5-element, as shown in the
following table:
Old Name:
|
input_copper
|
blast_furnace
|
slag_dump
|
tank
|
output_product
|
New Name:
|
smelter(1)
|
smelter(2)
|
smelter(3)
|
smelter(4)
|
smelter(5)
|
For example, the current state of the smelter might look like this
after running for a few shifts
smelter
smelter =
10.0000
13.3950
0 9.3750 7.2300
Furthermore, notice that each of the "streams" of material (raw input,
slag, etc) has a comes from a single "producer" and goes to a single
"consumer". Thus, we can identify each "stream" produced by an object
by the number assigned to its consumer. In other words, even though the
blast furnace produces only three outputs, we should call them blast_out(1)
through blast_out(5)
so we know where they are going. In this case, our previous
Matlab command would be rewritten like this:
blast_out
=
smelter(2)
*
[0.0
0.25
0.0 0.75 0.0]
blast_out =
0 2.5000 0 7.5000 0
Similarly, we would represent the result of one processing step at the
electrolysis tank as:
tank_out
=
smelter(4)
*
[0.0
0.036
0.0 0.0 0.964]
tank_out =
0 0.2700 0 0 7.2300
For the remaining locations in the smelter, the result of one
processing step is very easy. Everything at the input stockpile is
loaded into the blast furnce, like this:
stockpile_out
=
smelter(1)
*
[0.0 1.0
0.0 0.0 0.0]
stockpile_out
=
0 10.0000 0 0 0
(I know the workers will refill the stockpile with a new input material,
but right now I'm focussing my attention on the movment of existing
material within the smelter. We will return come back to the input in a
few minutes.) On
the other hand, everything at the slag dump and product shipping area
is permanently removed from the system. Since none of the material
currently at either smelter(3) and smelter(5) is still somewhere inside
the smelter one shift from now, we can represent the those parts of the
process as a multiplication by a vector of zeros.
Let us now stack up these
"processing vectors" for each smelter location to form a two
dimensional matrix with location 1 (input stockpile) forming row 1 and
the product shipping area forming row 5:
shift =
[0 1.0 0
0 0
0
0.25 0 0.75 0
0
0
0
0 0
0
0.036
0
0
0.964
0
0
0
0
0]
Notice that we can use the colon operator to select a specific row from
this matrix:
shift(4,:)
ans =
0
0.0360
0
0
0.9640
and thus we can rewrite the previous command for the electrolysis tank
as:
tank_out = smelter(4) *
shift(4,:)
tank_out
=
0 0.2700 0 0 7.2300
More generally, let us now repeat this "trick" to generate the outputs
from one processing step at each of the five objects in the smelter
model:
stockpile_out = smelter(1) *
shift(1,:); % notice the semicolons to suppress
output
blast = smelter(2) *
shift(2,:);
slag_out = smelter(3) *
shift(3,:);
tank_out = smelter(4) *
shift(4,:);
product_out
= smelter(5) *
shift(5,:);
Clearly, we can find the input to some "target" object at the next
processing step, by summing all outputs generated in the current
processing step that are sent directly to the "target" object. For
example, if object 2 (the blast furnace) is our "target" object, then
its input for the next shift must be:
stockpile_out(2) +
blast(2) + slag_out(2) + tank_out(2) + product_out(2)
Fortunately, we can use matrix operations to avoid having to deal with
all these tedious details. More specifically, let's now go back and
look at the outputs generated by the "trick" a few lines ago. (Notice
how I used the disp(
) command, so we see only the values of each variable, which is
a 5-element row vector, without showing any of the variable
names.)
disp(stockpile_out),
disp(blast),
disp(slag_out),
disp(tank_out),
disp(product_out)
0
10 0
0 0
0
3.3487
0
10.0463
0
0
0
0
0 0
0
0.3375
0
0 9.0375
0
0
0
0 0
To convert this two-dimensional table of values into the contents of
the kth
object in the smelter model at the next processing step, we must add
together every element in the kth column.
Using vector notation, we can do this simultaneously for every object
in a single Matlab expression, like this:
stockpile_out +
blast + slag_out + tank_out + product_out
ans =
10.0000
13.6862 0
10.0463 9.0375
So here is the bottom line for all of the discussion above. The way we
got from the 5-element row vector smelter
and 5x5 matrix shift was to
multiply the rows of shift by the
corresponding element from the vector smelter to form
a 5x5 table of results, and then "flattening" the table by adding the
elements in each column. This entire
series of steps is exactly what happens automatically when we apply
ordinary matrix multiplication to vector smelter and array shift.
Thus, all we really needed to do
to model the operation of the smelter is the following. To move forward
in time by one shift, we must redistribute the contents of smelter (i.e.,
the material currently in the system) by multiplication by the shift matrix,
then adding the the vector input
(representing the new material added from the stockpile every shift),
like this:
>> input=[10 0 0
0 0], smelter=input
input =
10 0
0 0 0
smelter =
10 0
0 0 0
>> smelter=smelter*shift+input
smelter =
10 10
0 0 0
>> smelter=smelter*shift+input
smelter =
10.0000
12.5000
0
7.5000 0
>> smelter=smelter*shift+input
smelter =
10.0000
13.3950
0 9.3750 7.2300
>> smelter=smelter*shift+input
smelter =
10.0000
13.6862 0
10.0463 9.0375
>> smelter=smelter*shift+input
smelter =
10.0000
13.7832 0
10.2647 9.6846
>>
We can keep going forward like this, one shift at a time, way for as
long as we like. However, the obvious question is what happens a very
long time in the future? Is there a long-term
"steady-state" distribution of material in the smelter over a shift,
and if so, how do we find it?
The answer to this question is very simple in Matlab, if you apply what
you know about how to find the sum of a (scalar) geometric
series. In other words, suppose I make n new friends every day, but
at the same time loose a fraction (1-p) of my existing friends because I
don't pay enough attention to them. How many total friends will I have
in the distant future? Clearly I will have n from today, n*p from
yesterday, n*p^2
from two days ago, etc, giving me a total of n/(1-p).
Similarly, the contents of the smelter will include input from the
current shift, input*shift
remaining from the previous shift, (input*shift)*shift
remaining from two shifts ago, etc., which is just another geometric
series, which can be solved in the same way to give:
>> input/(eye(5)-shift)
ans =
10.0000
13.8313 0
10.3734 10.0000
>>

