Algorithm analysis

# CS 10C - Algorithm analysis

![:newline]

.Huge[*Prof. Ty Feng*]

![:newline]

.Large[UC Riverside - WQ 2026]

![:newline 6]

![:scale 50%](../utils/style/ucr_cs_logo.png)

???

- Lecture topic about Big-O
    - Mathematical notation that characterizes the behavior of a function
      according to its argument
    - We use this notation in CS to classify algorithms, in terms of running
      time or memory space requirements, and according to the size of the input
      data
    - But we will take our time to get there
- Look at the issue of algorithm analysis from different angles first
- Follow three steps
    - First we'll try to see why we need algo analysis in the first place
        - 2 examples for that
    - Then we'll see two approaches
        - experimental and mathematical
    - And finally we'll get to Big-O

---

# Introduction

---

## Predicting efficiency?

.lcol[
### Use-case: classroom scheduling
- Preliminary testing shows it can schedule 10 classrooms in 1.42 seconds!

![:newline]

- Is the program efficient?
- Should UCR buy it?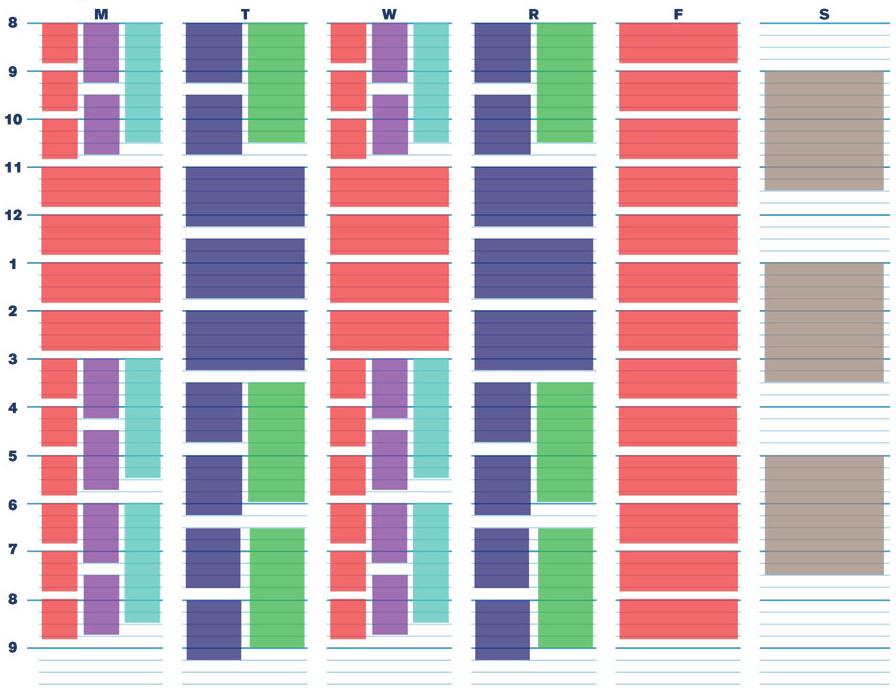
]

???

- Not enough information to describe the problem we want to solve
    - if we did have 10 rooms, we'd have the answer, but is it our case?
    - eg interview at google, ask for more details about the problem

![:flush 1]

.lcol[
#### Issues
- How will it perform in real conditions?
- With UCR's 110 classrooms (and thousands of courses)...
]

???

![:newline]
- So now, we have more details about the real problem
    - How can we know now how will the program perform with 110 classrooms?
    - We don't!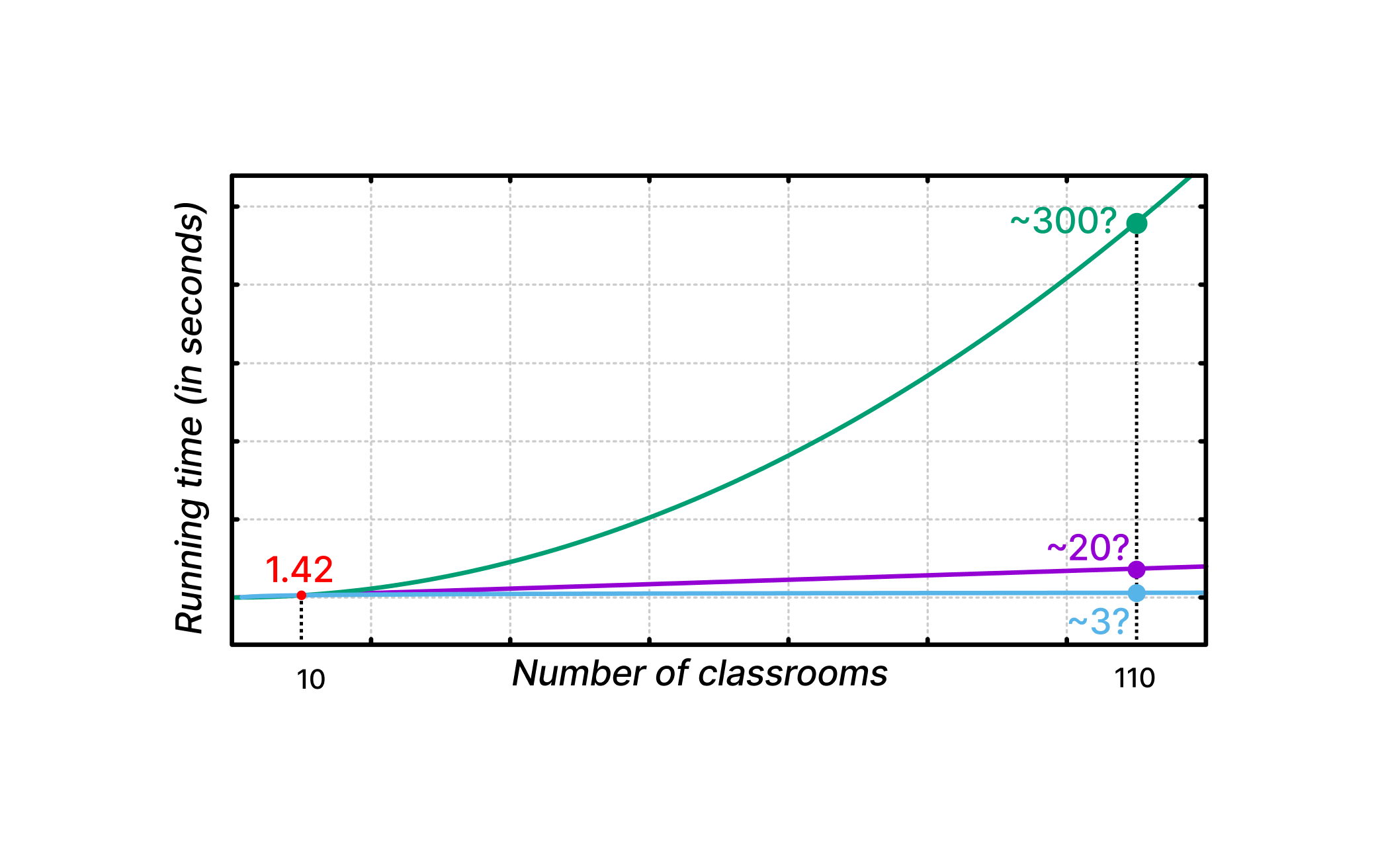

???

![:newline]
- Assuming the program runs around one algorithm
- Overall, depends on how the internal algorithm behaves
- Need a way to describe these curves
    - It would take about 3 seconds to schedule with an O(\log N) algo
    - It would take about 20 seconds to schedule with an O(N) algo
    - It would take about 300 secs (5 min) to schedule with an O(N^2) algo
![:newline]
- Here, prediction of a program or algorithm, what about comparing algorithms?

---

## Comparing algorithms?

### Use-case: searching a number in a sorted list of numbers

![:newline 2]

???

- Just definition of linear search
    - go through all items from start to end
- What would be a better algorithm that takes advantage from the nature of the
  list? ie the fact it's sorted

???

![:newline]
- At every step, discard all of the remaining items
- Which one if the best?
- Is it always the best?
    - What if we were to look for number 6?
- So maybe we need to compare their best-case and worst-case scenario?

???
![:newline]
- Worst-case: linear because all the items

.rcol[
![:newline 2]
- *Best-case:* Middle of list!
- *Worst-case:* Scan half of remaining sub-list at each step
]

???
![:newline]
- Worst-case: logarithmic (population is divided after 2 at each step)

![:flush 2]

#### Issues
- Is there a better way to express each algorithm's characteristics?

---

## Algorithm analysis

1. Predict performance
    - What should be the running time of my program if the amount of input data
      change?
    - What about the memory occupation?

???

- Reasons we'd like Algorithm analysis

--
1. Compare algorithms
    - Before starting a costly implementation, can we ensure a specific
      algorithm is better than an other?
    - Can we define "better"?
--
1. Characterize
    - What is the worst-case efficiency?
    - Average-case? Best-case?
--

![:newline 2]

### UCR courses
- **Informal approach** in 10C
- More formal approaches in advanced classes such as CS 141

???

![:newline]
- So let's see how we can analyse algorithms
    - first experimentally
    - then mathematically

---

# Experimental approach

---

## 3-SUM problem

In a set of N integers, how many (unique) triplets sum to zero?

![:newline 2]

![:scale 80%](images/3sum_intersection.svg)
.center.footnotesize[Intersection of 3 lines in a plane]
]

???

- Associated to many problems related to *computational geometry*
    - set of lines in the plane, are there three that meet in a point?
    - etc.
    - it's become its own class of problems called 3sum-hard

```terminal
$ cat 8ints.txt
30 -40 -20 -10 40 0 10 5

$ ./3sum < 8ints.txt
Number of triplets: 4
```
]

![:newline 2]

| a[i] | a[j] | a[k] | sum
| ---- | ---- | ---- | ---
| 30   | -40  | 10   | 0
| 30   | -20  | -10  | 0
| -40  | 40   | 0    | 0
| -10  | 0    | 10   | 0

]

---

## Brute-force algorithm

```C
int Count3Sum(const std::vector<int> &a) {
  int N = a.size();
  int count = 0;

for (int i = 0; i < N; i++)
    for (int j = i + 1; j < N; j++)
      for (int k = j + 1; k < N; k++)
        if (a[i] + a[j] + a[k] == 0)
          count++;

return count;
}

int main(void) {
  int n;
  std::vector<int> a;

while (std::cin >> n)
    a.push_back(n);

std::cout << "Number of triplets: "
      << Count3Sum(a) << std::endl;

return 0;
}

```

![:filename](3sum.cc)

]
]

???

- Explain program
- Mention program on Canvas
- Mention reference argument

---

## Timing measurement .ref[\*]

Multiple runs, each with a different amount of data:

```terminal
$ time ./3sum < 1Kints.txt
Number of triplets: 644996
./3sum < 1Kints.txt `0.98s user` 0.00s system 99% cpu 0.983 total
```

???

- Mention use of `time`

```terminal
$ time ./3sum < 2Kints.txt
Number of triplets: 5344063
./3sum < 2Kints.txt `7.82s user` 0.00s system 99% cpu 7.828 total

```

```terminal
$ time ./3sum < 4Kints.txt
Number of triplets: 41964881
./3sum < 4Kints.txt `62.66s user` 0.00s system 99% cpu 1:02.68 total

```

```terminal
$ time ./3sum < 8Kints.txt
Number of triplets: 342566644
./3sum < 8Kints.txt `500.52s user` 0.00s system 100% cpu 8:20.50 total
```

![:newline 0.5]

- Somewhat difficult to comprehend...
- Let's plot for better visualization!

---

## Plot (standard)

Running time \$T(N)\$ vs input size \$N\$

![:scale 80%](images/3sum_std.svg)

![:newline]

- So, not a linear progression...
- Can we predict the running time for even larger input (e.g. 16K)?

???

- Back to the classroom scheduling problem, how do we predict a data point?
- Let's change the plot and see if it helps

---

## Plot (log-log)

Running time \$T(N)\$ vs input size \$N\$ on a **log-log plot**

???

- Represent both x and y axes on log scale

???

![:newline]
- Linear equation
    - m is the slope of the line
    - b is the y intercept

???

![:newline]
- lg is binary logarithm
    - x = log2(n) <=> 2^x = n

.rcol[
![:newline]
Find the slope and intercept:
- \$m = \frac{\lg(y_2/y_1)}{\lg(x_2/x_1)} \approx 2.9978\$
- \$b = \lg(y) - 2.9978 * \lg(x) \approx -30.00\$
]

???

![:newline]
- By taking two data points on the line, we can find both values
    - Note that values are truncated because many decimals

.rcol[
![:newline 2]
Now, can translate back into equation on standard scale:
- \$T(N) = N^m * 2^b\$
- \$T(N) = N^{2.9978} * 2^{-30.00}\$
]

???

![:newline]
- Standard formula to get back to monomial equation
    - Monomial is a polynomial which has only one term

![:newline]
- \$\lg(T(N)) = m * \lg(N) + b\$
- \$2^{\lg(T(N))} = 2^{m\*\lg(N) + b}\$
- \$T(N) = 2^{m\*\lg(N)} * 2^{b}\$
- \$T(N) = (2^{\lg(N)})^m * 2^{b}\$
- \$T(N) = N^m * 2^{b}\$

---

## Back to standard plot

Running time \$T(N)\$ vs input size \$N\$

![:scale 80%](images/3sum_std.svg)

![:newline]
- \$T(N) = N^m * 2^b\$
- \$T(N) = N^{2.9978} * 2^{-30.00}\$

???
- So now that we finally have an equation, let's get back to our original
  question
- Can we predict the running time for input 16K?

---

## Validation of prediction?

- Hypothesis:
    \\[T(N) = N^{2.9978} * 2^{-30.00}\\]
- Predictions:
    - For N = 8K, running time should be about *502 seconds (08m:22s)*
    - For N = 16K, running time should be about *4122 seconds (01h:08m:42s)*

![:newline 2]

- Experiments:

```terminal
    $ time ./3sum < 8Kints.txt
    ...
    ./3sum < 8Kints.txt `500.52s user` 0.00s system 100% cpu 8:20.50 total

$ time ./3sum < 16Kints.txt
    ...
    ./3sum < 16Kints `4132.14s user` 0.00s system 99% cpu 1:08:52.42 total
    ```

Hypothesis is validated!

???

- If using non-truncated values, hypothesis is even more validated because
  predictions are very close than here!

---

## Conclusion

### Issues

- Need to actually implement the algorithm in order to characterize it
  experimentally!

- Difficult to get precise measurements as it heavily depends on:
    - The input data
    - The hardware (CPU, memory, caches, etc.)
    - The software (compiler, garbage collector, etc.)
    - The system (OS, network, etc.)

- Require to run a significant (potentially huge) number of experiments to
  gather data points

![:newline 2]

- Need for a better model...!

---

---

layout:false

# Recap

## Experimental approach

```C
int Count3Sum(const std::vector<int> &a) {
  int N = a.size();
  int count = 0;

for (int i = 0; i < N; i++)
    for (int j = i + 1; j < N; j++)
      for (int k = j + 1; k < N; k++)
        if (a[i] + a[j] + a[k] == 0)
          count++;

return count;
}

```

![:filename](3sum.cc)

]
]

.rcol[
### Measurements
.tiny[
```terminal
$ time ./3sum < 1Kints.txt
Number of triplets: 644996
./3sum < 1Kints.txt `0.98s user`...
```
```terminal
$ time ./3sum < 2Kints.txt
Number of triplets: 5344063
./3sum < 2Kints.txt `7.82s user`...
```
```terminal
$ time ./3sum < 4Kints.txt
Number of triplets: 41964881
./3sum < 4Kints.txt `62.66s user`...
```
]
...and so on...
]

![:flush 0.5]

### Model
![:scale 100%](images/3sum_std.svg)

]

.rcol66[
### Conclusion
- Can now predict running time for N = 16K **without running it!**
    - *4122 seconds (01h:08m:42s)*, which can be confirmed
.tiny[
```terminal
$ time ./3sum < 16Kints.txt
...
./3sum < 16Kints `4132.14s user`...
```
]
- Still needs to implement/run algorithm to get measurements
- Need for a better model
]

---

# Mathematical approach

---

## Idea

- Total running time is  sum of *(cost x frequency)* for all operations

\\[\displaystyle\sum\_{op} cost(op) * freq(op)\\]

???

- Cost would be the number of nanoseconds every operation takes
    - add, multiply, divide, etc. between integers
    - same for floating-point
    - variable declaration, assignment statement, comparisons, array access,
      etc.
    - etc.

## Issues

- Need to analyse entire program to determine all the actual operations
- Actual cost depends on computer, compiler
- Actual frequency depends on algorithm, input data
- Might be very complicated overall...

![:newline 2]

## Simplification

- Count number of statements
- As a function of input size \$N\$

???

![:newline 2]
- Count number of statements
- and see how it relates to the input size
- Let's take an example!

---

## 1-SUM

```C
  int count = 0;

for (int i = 0; i < N; i++)
    if (a[i] == 0)
      count++;

return count;

```

![:filename](1sum.cc)

]

???

- Make students do the count in class

.rcol.small.center[

| Statement          | Frequency            |
| ------------------ | -------------------- |
| `int count = 0;`   | \$1\$              |
| `int i = 0;`       | \$1\$              |
| `i < N;`           | \$N + 1\$          |
| `i++;`             | \$N\$              |
| `if (a[i] == 0)`   | \$N\$              |
| `count++;`         | \$0\$ to \$N\$   |
| `return count;`    | \$1\$              |

]

???

- What's the worst-case scenario
    - => the entire array is 0
- Now what's the estimated running time?

![:flush 2]
Estimated running time (worst-case):
- \$T(N) = 4N + 4\$

---

## 2-SUM

.lcol.small[

```C
  int count = 0;

for (int i = 0; i < N; i++)
    for (int j = i + 1; j < N; j++)
      if (a[i] + a[j] == 0)
        count++;

return count;

```

![:filename](2sum.cc)

.small[
- How to compute the frequency of the inner loop?
- Sum of series (Gauss)
    \$M+...+2+1 = \frac{1}{2}M(M+1)\$
]
]

.rcol.scriptsize.center[

| Statement                 | Frequency                            |
| ------------------------- | ------------------------------------ |
| `int count = 0;`          | \$1\$                              |
| `int i = 0;`              | \$1\$                              |
| `i < N;`                  | \$N + 1\$                          |
| `i++;`                    | \$N\$                              |
| `int j = i + 1;`          | \$N\$                              |
| `j < N;`                  | \$\frac{1}{2}N(N+1)\$              |
| `j++;`                    | \$\frac{1}{2}(N-1)N\$              |
| `if (a[i] + a[j] == 0)`   | \$\frac{1}{2}(N-1)N\$              |
| `count++;`                | \$0\$ to \$\frac{1}{2}(N-1)N\$   |
| `return count;`           | \$1\$                              |

]

![:flush 0]

Estimated running time (worst-case):
- \$T(N) = 2N^2 + N + 4 \$
- Was difficult to compute...

???

- Need to simplify some more
    - Maybe don't need to count all the statements separately

---

## Simplify some more

.lcol[
- Identify the operation that represents the overall running time the best
    - Usually the body of the inner loop
    - \$\frac{1}{2}N(N-1) = \frac{1}{2}N^2 - \frac{1}{2}N\$
]
.rcol.small[
```C
for (int i = 0; i < N; i++)
    for (int j = i + 1; j < N; j++)
*        if (a[i] + a[j] == 0)
            count++;
```
]

![:flush 1]

.lcol[
- Could we ignore the lower order terms?
    - \$\frac{1}{2}N^2 - \frac{1}{2}N\$
    - \$\sim \frac{1}{2}N^2\$
]

???

- What do you think?
    - When n becomes large enough, n2 totally takes over
    - Keep only *leading term*

???

- Some people mainly use the tilde notation to talk about algorithm analysis

.lcol.small[
![:newline 2]
- Tilde notation
    - \$f(N) \sim g(N)\$ means \$\displaystyle\lim\_{N \rightarrow
      \infty}\frac{f(N)}{g(N)} = 1\$
]

---

## Tilde approximation and order of growth

![:newline 1]

.center[
| Function                                               | Tilde approximation        | Order of growth   |
| ------------------------------------------------------ | -------------------------- | ----------------- |
| \$\frac{1}{6}N^3 - \frac{1}{2}N^2 + \frac{1}{3}N\$   | \$\sim\frac{1}{6}N^3\$   | \$N^3\$         |
| \$\frac{1}{2}N^2 - \frac{1}{2}N\$                    | \$\sim\frac{1}{2}N^2\$   | \$N^2\$         |
| \$\lg N + 1\$                                        | \$\sim \lg N\$           | \$\lg N\$       |
| \$3\$                                                | \$\sim 3\$               | \$1\$           |
]

???

- Drop constant in the leading term, if any

![:newline 2]

## Conclusion

1. In principle, accurate mathematical models are available
1. In practice, approximate models do a good job: \$T(N) \sim cN^x\$
1. For the mass, *order of growth* is usually enough...

???

![:newline]
- Approximate models for people who study the theory of algorithms
- So how does this order of growth matches actual code?

---

# Order-of-growth classification

---

## Typical set of functions describing common algorithms

--
![:flush 0.5]
.lcol[
- **Logarithmic** \$(\log N)\$
    - Divide in half
]
.rcol[
```C
while (N > 1) { N = N / 2; ... }
```
]

--
![:flush 0.5]
.lcol[
- **Linear** \$(N)\$
    - Simple loop
]
.rcol[
```C
for (int i = 0; i < N; i++)
```
]

--
![:flush 0.5]
.lcol[
- **Linearithmic** \$(N \log N)\$
    - Divide and conquer
]
.rcol[
```C
[see mergesort lecture]
```
]

???

- Linearithmic in two words
    - Divide data set in two repetitively, then merge linearly

--
![:flush 0.5]
.lcol[
- **Quadratic** \$(N^2)\$
    - Double loop
]
.rcol[
```C
for (int i = 0; i < N; i++)
    for (int j = 0; j < N; j++)
```
]

--
![:flush 0.5]
.lcol[
- **Cubic** \$(N^3)\$
    - Triple loop
]
.rcol[
```C
for (int i = 0; i < N; i++)
    for (int j = 0; j < N; j++)
        for (int k = 0; k < N; k++)
```
]

--
![:flush 0.5]
.lcol[
- **Exponential** \$(2^N)\$/**Factorial** \$(N!)\$/etc.
    - Exhaustive search
]
.rcol[
```C
f(k) = f(k-1) + f(k-2) // k > 1
```
]

???

- Travelling salesperson problem
    - list of cities, trying to find the shortest route to visit all the cities
      and get back to origin city?
    - Try all the combinations!

---

# Recap

## Mathematical approach

.lcol[
### Counting statements (1)
.footnotesize[
```C
for (int i = 0; i < N; i++)
*   if (a[i] == 0)
        count++;
```
]
]

![:flush 1]

.lcol[
### Counting statements (2)
.footnotesize[
```C
for (int i = 0; i < N; i++)
    for (int j = i + 1; j < N; j++)
*        if (a[i] + a[j] == 0)
            count++;
```
]
]

.rcol[
#### Estimate running time
- \$\frac{1}{2}N^2 - \frac{1}{2}N\$
- Tilde notation: \$\sim \frac{1}{2}N^2\$
- Order of growth: \$N^2\$
]

![:flush 1]

## Common programming pattern vs order of growth
.lcol[
- Constant
.scriptsize[
```C
a = b + c;
```
]
- Logarithmic
.scriptsize[
```C
while (N > 1) { N = N / 2; ... };
```
]
- Linear
.scriptsize[
```C
for (int i = 0; i < N; i++)
```
]
]
.rcol[
- Linearithmic
    * See later...
- Quadratic
.scriptsize[
```C
for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++)
```
]
- Etc.
]

---

# Order-of-growth classification

---

## Visual representation

![:scale 85%](images/order-of-growth.svg)

---

## Practical implications

- Assume a computer with a 1 GHz processor (and IPC of 1),  
  and an input size $N$ of 100,000.
![:newline 0.5]
- How long would it take to process the input according to different algorithm's
  growth rates?
![:newline 0.5]

???

- 100,000 is not that big
    - population of Richmond, CA
    - number of neurons in a lobster

.center[
| Growth rate    | Running time               |
| -------------- | ---------------------      |
| Logarithmic    | $1.7e^{-8}$ seconds        |
| Linear         | $0.0001$ seconds           |
| Linearithmic   | $0.00166$ seconds          |
| Quadratic      | $10$ seconds               |
| Cubic          | $11$ days                  |
| Exponential    | $3.17 * 10^{30086}$ years! |
]

???

- Logarithmic
    - lg(100,000) = ~17
    - 17 / 1e9 => 1.7e-8 sec
- Linear
    * 100,000 / 1e9 => 0.0001 sec
- Linearithmic
    * 100,000 lg (100,000) = 1,700,000
    * 1,700,000 / 1e9 = 0.0017 sec
- Quadratic
    * 100,000^2 = 10,000,000,000
    * 10000000000/1e9 = 10 sec
- Etc.

---

---

# Recap

## Mathematical approach

.lcol[
### Counting statements
.footnotesize[
```C
for (int i = 0; i < N; i++)
    for (int j = i + 1; j < N; j++)
*        if (a[i] + a[j] == 0)
            count++;
```
]
]
.rcol[
### Estimate running time
- \$\frac{1}{2}N^2 - \frac{1}{2}N\$
- \$\sim \frac{1}{2}N^2\$
- Order of growth: \$N^2\$
]
.lcol[
![:newline 2]

### Order of growth
![:scale 100%](images/order-of-growth.svg)
]
.rcol[
![:newline 1]

### Implications
.footnotesize[
- 1GHz processor, input size N=100,000

]

---

---

## Definition

- Most usual notation for describing computational *complexity* of algorithms
- Indicates **upper** *asymptotic* bound, using order-of-growth classification

![:newline]

## Formal definition

- \$T(N)\$ is \$O(F(N))\$ if there exist  
\$c > 0\$ and \$n\_0 > 0\$ such  as  
\$T(N) \leq cF(N)\$ when \$N \geq n\_0\$

--
.rcol33[
![:scale 100%](images/big_o_example.svg)
]

.lcol66[
To prove $3N^2+2N+4 = O(N^2)$, you need to find $c$ and $n_0$ such that:
- $3N^2+2N+4 \leq cN^2$
- $3N^2 \leq 3N^2$, $2N \leq 2N^2$, $4 \leq 4N^2$
- $3N^2+2N+4 \leq 9N^2$ for $N \geq 1$
- Therefore, for $c = 9$ and $n_0 = 1$, $3N^2+2N+4 \leq 9N^2$ when $N \geq n_0$. $T(N) = O(N^2)$. 
]

---

## Big-Ω (*omega*)

- Same idea as Big-O but indicates **lower** bound
- \$T(N)\$ is \$\Omega(F(N))\$ if there exist \$c > 0\$ and \$n\_0 > 0\$
  such as \$T(N) \geq cF(N)\$ when \$N \geq n\_0\$

???

- Introduce notion that sometimes big-o and big-omega can be misused or
  confusing or even not precise enough
- Eg 3-SUM is big-omega(1), or 1-SUM is O(N4)
- So sometimes, need a more precise notation: big-theta

![:newline 2]

## Big-Θ (*theta*)

.lcol66[
- Asymptotic **tight** bound
- \$T(N)\$ is \$\Theta(F(N))\$ if \$T(N)\$ is both
    - \$O(F(N))\$ **and** \$\Omega(F(N))\$
    - There exist \$c_1 > 0\$ and \$c_2 > 0\$ and \$n\_0 > 0\$ such as
      \$T(N) \geq c_1F(N)\$ and \$T(N) \leq c_2F(N)\$ when \$N \geq n\_0\$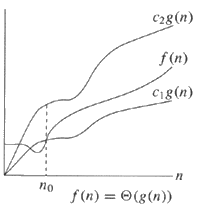
]

---

### Big-O is *only* an upper bound

- $3N^2+2N+4 = O(N^2)$
]

--
.lcol75[
- And also $O(N^3)$, and $O(N^4)$, and $O(N!)$
]

--
.lcol75[
![:newline]
### Equality vs inclusion

- $O(N) = O(N^2)$ but $O(N^2) \neq O(N)$
    - $=$ is assumed unidirectional
]

--
.lcol75[
- $\in$ is considered a better and non-ambiguous notation
    - $O(N) \in O(N^2)$
]

- Can't all functions be in Big-Θ of something?
]

--
.rcol33[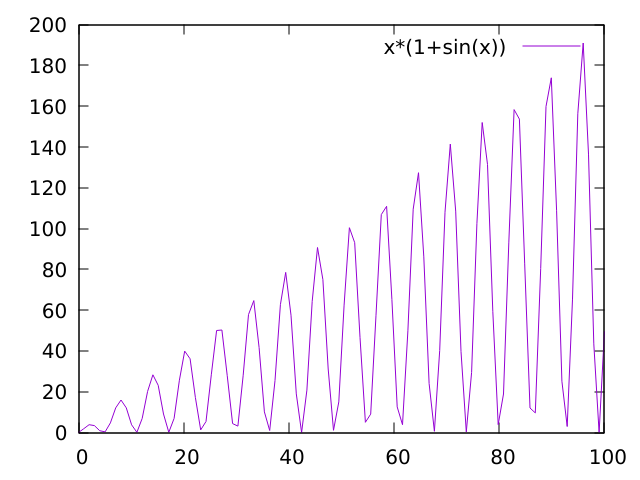
![:scale 100%](images/non_theta_example.png)
]
.lcol66[
- $f(N) = N (1 + sin(N))$
    - $\in O(N)$ and $\in \Omega(0)$
    - $\notin \Theta(N)$ and $\notin \Theta(0)$
]

---

## Algorithm complexity, in practice...

- Be aware of the mathematical background and notations
    - But using Big-O is usually good enough
- Ignore lower order terms and drop the leading term's coefficient!
    - E.g. \$T(N) = 4N^2 + N + 3\$ is considered to be \$O(N^2)\$

???

- Has to be the tightest upper bound

![:newline 1]

```C
  for (int i = 0; i < N; i++)
    if (a[i] == 0)
      count++;

```

![:filename](1sum.cc)

]
![:flush]
.lcol[
- 2-SUM: \$T(N) = O(N^2)\$
]
.rcol.footnotesize[

```C
  for (int i = 0; i < N; i++)
    for (int j = i + 1; j < N; j++)
      if (a[i] + a[j] == 0)
        count++;

```

![:filename](2sum.cc)

]
![:flush]
.lcol[
- 3-SUM: \$T(N) = O(N^3)\$
]
.rcol.footnotesize[

```C
  for (int i = 0; i < N; i++)
    for (int j = i + 1; j < N; j++)
      for (int k = j + 1; k < N; k++)
        if (a[i] + a[j] + a[k] == 0)
          count++;

```

![:filename](3sum.cc)

]

---

## Some pitfalls...

![:newline 1]

### $O(N^2)$?
.lcol66[
```C
for (int i = 0; i < N; i++) {
    for (int j = 0; j < 5; j++) {
        ...
    }
}
```
]

--
.rcol33[
- No, $O(N)$
- Innermost loop is constant!
]

![:flush 2]

### $O(N^2)$?
.lcol66[
```C
for (int i = 0; i < N; i++) {
    if (i == (N - 1)) {
        for (int j = 0; j < N; j++) {
            ...
        }
    }
}
```
]

--
.rcol33[
- No, $O(N)$
- Innermost loop is executed only once
]

???

- becomes 2N and not N2

![:newline 1]
- Live quiz here!

---

## Function calls (1)

```C
double sum_squares(int count) {
    double sum = 0.0;

for (int i = 0; i < count; i++)
        sum += std::sqrt(i);

return sum;
}
```

- We know that the for loop is $O(N)$
- What about the function call to `std::sqrt()`?

???

- sqrt
    - can be a processor instruction directly
    - or a software implementation
        - requires a few iterations regardless of the number to converge

![:newline 2]

### Complexity

- Substitute Big O for that function
    - E.g. `std::sqrt()` is usually considered as $O(1)$
- Result: function `sum_squares()` is $O(N)$

---

## Function calls (2)

```C
bool str_contains(std::string str, std::string pattern)
{
    for (int i = 0; i < str.length() - pattern.length(); i++)
        if (!std::strncmp(str + i, pattern, pattern.length()))
            return true;
    return false;
}
```

- We know that the loop is $O(N)$
- What about the function call to `std::strncmp()`?

![:newline 2]

### Complexity

- By examining the parameters, complexity depends of input size (`pattern,
  pattern.length()`)
- Result: function `str_contains()` is $O(N^2)$

---

## Log

.lcol.footnotesize[

```C
int BSearch(const std::vector<int> &array,
            int key) {
  int lo = 0, hi = array.size() - 1;

while (lo <= hi) {
    int mid = lo + (hi - lo) / 2;

if (array[mid] == key)
      return mid;

if (array[mid] < key)
      lo = mid + 1;
    else
      hi = mid - 1;
  }

return -1;
}

```

![:filename](binary_search.cc)

]

.rcol[
### Observations
- Divides the input data by 2 at each iteration
- Until it finds the searched item (or doesn't)
]

???

- Show the math
    * Iteration 1: N
    * Iteration 2: N/2
    * Iteration 3: N/4
    * ...
    * Iteration m-1: 2
    * Iteration m: 1

### Do the math
- $N$ is the size of the input data
- $x$ is the number of iterations
- $\frac{N}{2^x} = 1$
- $\Rightarrow x = \log_2(N)$
]

![:flush 1]

### Complexity
- Result: function `bsearch()` is $O(\log_2 N)$

- FYI, this function exists as a standard function!
.footnotesize[
```C
std::binary_search(array.begin(), array.end(), key);
```
]

---

# Space complexity

---

## Intro

- Estimate how much memory an algorithm uses
    - Input space: space taken by the algorithm's input values
    - *Auxiliary* space: temporary extra space used during the execution
- Count number of variables and their size
- Is total amount of memory related to input size N?

![:newline]

|       Type name | Size on computers (GNU/Linux/x86_64) |
|----------------:|:------------------------------------------|
|          `char` | 1 byte (8 bits)                           |
|     `short int` | 2 bytes (16 bits)                         |
|           `int` | 4 bytes (32 bits)                         |
|      `long int` | 8 bytes (64 bits)                         |
| `long long int` | 8 bytes (64 bits)                         |
|         `float` | 4 bytes (32 bits)                         |
|        `double` | 8 bytes (64 bits)                         |
|         `void*` | 8 bytes (64 bits)                         |

]

---

## Examples (1)

.rcol.footnotesize[

```C
int CountLetter(const std::string &str,
                const char letter) {
  int count = 0;

for (auto c : str)
    if (c == letter)
      count++;

return count;
}

```

![:filename](count_letter.cc)

]

???

- Talk about code
    - c++11, for auto loop
    - Why const?

.lcol[
- Input size is $N$ characters
- Fixed amount of additional variables regardless of input's size
- Overall memory complexity is $O(N) + O(1) = O(N)$
]

![:flush 1]

## Examples (2)

.rcol66.footnotesize[

```C
std::string StrUppercase(const std::string &input) {
  std::string output = input;

for (auto &c : output)
    c = std::toupper(static_cast<unsigned char>(c));

return output;
}

```

![:filename](uppercase.cc)

]

???

- Talk about code
    - copy string
    - why reference in for loop? to modify each character of the string itself
    - static cast to meet toupper()'s expectation (otherwise undefined behavior)

.lcol33[
- Input size is $N$ characters
- Extra memory allocation proportional to input's size
]
.wide[
- Memory complexity is $O(N) + O(N) = O(N)$
]