Lists

# CS 10C - Lists

![:newline]

.Huge[*Prof. Ty Feng*]

![:newline]

.Large[UC Riverside - WQ 2026]

![:newline 6]

![:scale 40%](../utils/style/ucr_cs_logo.png)

---

# Abstract Data Types

## Terminology

### Type
- Collection of values
- E.g.: boolean (`true`/`false`), int (`..., -1, 0, 1, ...`), float, etc.
	- Simple type: no subparts
	- Aggregate/composite type: record containing fields (`struct { ... }`)

???

- simple type:
    - aka trivial types or basic types or primitive types
    - essentially types the processor knows at hardware level

![:newline 0.5]
### Data type
- Type and collection of operations to manipulate the type
- E.g.: `+ - * /`, `== != < >`, etc.

???

- data type: also operations that are known at processor level

![:newline 0.5]
### Abstract data type (ADT)
- Specification of data type, *independent of implementation*
- E.g.: **list**, stack, queue, dictionary, set, etc.

???
- ADT is defined as a type and a set of operations on it
    - Doesn't define how it's implemented
    - Implementation is hidden to the user
	- Can be changed transparently (e.g. for efficiency reasons)

- Why aren't `int`'s ADTs?
	- Can have different representations: binary most often as two's
	  complement, but can be binary-coded decimal or in ones' complement.
	- However the abstraction isn't perfect: users must be aware of issues like
	  arithmetic overflows which are due to the representation!

- Difference between list and set
    - List has a notion of order via indexing
    - Set has no order but is focused on membership (is a value a member of the
      set): then union between two sets, intersection, difference, etc.

![:newline 0.5]
### Data structure
- Implementation of an ADT
- E.g.: array, singly linked list, doubly linked list, hash	table, trees, etc.

???

Some of this terminology is not perfect:
- e.g., types and data types are often interchangeable
- however, ADTs and data structures are 100% correct!

---

# The List ADT

---

## Definition

- Ordered collection of items of some type `T`
]
.rcol25[
![:scale 80%](images/list.svg)
]

- Typical set of operations (*API*)
]

```C
// Return number of items in list
size_t Size();
// Return item at position @pos
const T& Get(const size_t pos);
// Return position of first occurence of @item (-1 if not found)
int Find(const T &item);
// Remove item at position @pos
void Remove(const size_t pos);
// Insert @item at position @pos
void Insert(const T &item, const size_t pos);
```

![:newline 1]

- Many other operations are possible, depending on the context and requirements:
  `isEmpty()`, `pushFront()`, `popBack()`, etc.

???

- Ask how each of the other operations can actually be implemented with the
  basic operations

---

## Typical implementations

.lcol60[
- Most commonly as arrays (*fixed* or *dynamic*)
]
.rcol40[
![:scale 100%](images/std_vector.svg)
]

--
![:flush 1]
.lcol60[
- Or linked lists (*singly* or *doubly linked*)
]
.rcol40[
![:scale 100%](images/std_forward_list.svg)
]

--
![:flush 1]
.lcol60[
- But possibly even as trees!
]
.rcol40[
![:scale 60%](images/list_tree.svg)
]

???

- Plenty of ways to implement the same ADT using various data structures!

---

# Fixed array implementation

---

--
![:flush 1]

--
![:flush 1]

--
![:flush 1]

--
![:flush 1]

???

- Important to notice that capacity does not change

---

## Data structure

.lcol.small[

```C
template <typename T>
class ListFixedArray {
 private:
  // Fixed capacity of 3 items
  static constexpr size_t capacity = 3;
  std::array<T, capacity> items;
  size_t cur_size = 0;

...
};

```

![:filename](list_fixed_array.h)

]

.rcol.small[
- `static` to make `capacity` exist without instantiating and `constexpr` to
  make it available to compiler
- `std::array` is equivalent to a C-style array (`T items[capacity]`)
- Member variables already initialized
]

???

- `std::array`
    - New since C++11

![:flush 2]

## Constructor/destructor

.lcol.small[

```C
 public:
  ListFixedArray() = default;
  ~ListFixedArray() = default;

```

![:filename](list_fixed_array.h)

]

.rcol.small[
- `default` to have the compiler generate the corresponding constructor or
  destructor:
    - No initialization list
    - Empty compound statement
]

???

- `default`
    - New since C++11

---

## List API (1/3)

```C
  size_t Size() {
    return cur_size;
  }

```

![:filename](list_fixed_array.h)

]

![:newline 0.5]
.small[

```C
  const T& Get(const size_t pos) {
    if (pos >= cur_size)
      throw std::out_of_range("Position out of range!");

return items[pos];
  }

```

![:filename](list_fixed_array.h)

]

![:newline 0.5]
.small[

```C
  int Find(const T &item) {
    for (size_t i = 0; i < cur_size; i++)
      if (items[i] == item)
        return i;
    return -1;
  }

```

![:filename](list_fixed_array.h)

]

![:newline 1]
- What is the complexity of each function?

---

## List API (2/3)

```C
  void Remove(const size_t pos) {
    if (pos >= cur_size)
      throw std::out_of_range("Position out of range!");

for (auto i = pos + 1; i < cur_size; i++)
      items[i - 1] = items[i];
    cur_size--;
  }

```

![:filename](list_fixed_array.h)

]

![:newline 2]
![:scale 70%](images/list_fixed_array_remove.svg)

---

## List API (3/3)

```C
  void Insert(const T &item, const size_t pos) {
    if (pos > cur_size)
      throw std::out_of_range("Position out of range!");
    if (cur_size == capacity)
      throw std::overflow_error("List full!");

if (pos != cur_size) {
      // Move existing item(s) if insertion before them
      auto i = cur_size - 1;
      do {
        items[i + 1] = items[i];
      } while (i-- != pos);
    }

items[pos] = item;
    cur_size++;
  }

```

![:filename](list_fixed_array.h)

]

![:newline 1]
![:scale 70%](images/list_fixed_array_insert.svg)

---

## Conclusion

Pros and cons?

![:newline 1]

### Pros

- Implementation is straight forward
- Little to no waste of memory space if number of items matches capacity of list
  on average

![:newline 1]

### Cons

- Waste of space if list mostly empty
- Really just an array, not an actual list
    - Insertion and removal operations are limited

---

---

.lcol[
## List ADT
- Ordered collection of items of some type `T`
![:scale 70%](images/list.svg)
]
.rcol[
## Various implementations
![:scale 70%](images/std_vector.svg)
![:scale 70%](images/std_forward_list.svg)
]
![:flush 0.5]
.lcol55[
## Fixed array implementation
.tiny[

```C
template <typename T>
class ListFixedArray {
 private:
  // Fixed capacity of 3 items
  static constexpr size_t capacity = 3;
  std::array<T, capacity> items;
  size_t cur_size = 0;

public:
  ListFixedArray() = default;
  ~ListFixedArray() = default;

// Return number of items in list
  size_t Size() {
    return cur_size;
  }
...
};

```

![:filename](list_fixed_array.h)

]
]
.rcol45[
## Pros and cons
- (+) Simple implementation
- (-) No flexibility, doesn't fully implement the List API
]

---

# Dynamic array implementation

---

## When to grow/shrink?

![:newline 1]

### Option #1: on each operation

- `Insert()`: increase size of array by 1
- `Remove()`: decrease size of array by 1

![:newline 0.5]
#### Problem
Resizing the array on each operation is too expensive!
- Need to copy all items to new array, for each operation
- To add first $n$ items, complexity would be $O(n^2)$

![:newline 2]
### Option #2: Infrequently

- Resizing must be a **rare** event
- But without wasting too much extra memory space...

---

## Resizable data structure

.lcol60.footnotesize[

```C
template <typename T>
class ListDynamicArray {
 private:
  // Initial capacity of 3 items
  size_t capacity = 3;
  std::unique_ptr<T[]> items;
  size_t cur_size = 0;
...
 public:
  ListDynamicArray() : items(std::unique_ptr<T[]>(new T[capacity])) { }
  ~ListDynamicArray() = default;
...
};

```

![:filename](list_dynamic_array.h)

]

.rcol40[
- `capacity` is no longer a constant
- Smart pointer for array of items
    - Ensures list is sole owner of the array
    - Auto-destruction when list disappears
]

???

- Default destructor takes care of automatic deallocation

.lcol60.footnotesize[

```C
  // Resize array according to new capacity
  void Resize(size_t new_cap) {
    assert(new_cap && new_cap >= cur_size);

std::unique_ptr<T[]> new_items(new T[new_cap]);
    std::move(items.get(),
              std::next(items.get(), cur_size),
              new_items.get());
    std::swap(items, new_items);
    capacity = new_cap;
  }

```

![:filename](list_dynamic_array.h)

]

.rcol40.small[
- `assert()` for checking internal invariants
- Efficient data transfer from one array to another with `std::move()`
- Efficient exchange of values between smart pointers with `std::swap()`
]

---
## Side Note: `std::move` in C++11

### The Performance Problem with Copies

.lcol60.small[
Traditional C++ made unnecessary copies:
```C++
vector<int> v(1000000);  // 1M elements

// Expensive copy!
vector<int> w = v;       // Copies all elements

void process(vector<int> data) {
  // ... use data ...
}
process(v);  // Another expensive copy!
```
]

.rcol40.small[
- Copying large objects is expensive
- Often we don't need the original anymore
- Temporary objects are copied then destroyed
- Wastes time and memory
]

![:flush 1]

### The Solution: Move Semantics

.lcol40.small[
Instead of copying, **transfer ownership** of resources from source to destination
- Source object becomes empty/invalid (but safe to destroy)
- Destination object takes over the resources
- No memory allocation or element-by-element copying needed
]

.rcol60.small[
Using `std::move`:
```C++
vector<int> v(1000000);  // 1M elements

// Cheap move (pointer swap), no element-by-element copy
std::vector<int> w = std::move(v);

void process(vector<int> data) {
  // ... use data ...
}
// Another cheap move into process's parameter
process(std::move(w));
```
]

---

## Growing strategy

- If array is full, create a new array of **twice** the size and copy items

```C
  void Insert(const T &item, const size_t pos) {
...
    // Grow by 2 when reaching max capacity
    if (cur_size == capacity)
      Resize(2 * capacity);
...
  }

```

![:filename](list_dynamic_array.h)

]

---

## Growing strategy: complexity analysis

**Example:** insert $(n+1)$ items at the end of list

![:newline 1]

### Usual Big-O analysis

For one insertion:
- Best case (*array still has room*): $O(1)$
- Worst case (*array has to be expanded first*): $O(N)$
- Average case (*?*): $?$

![:newline 1]
How can we be more precise and offer more guarantee?

???

- Worst-case is too pessimistic

![:newline 1]
### Amortized analysis

- $n$ operations take constant time: $O(1)$
- Last operation takes linear time: $O(n)$
- Total time: $T(n+1)=nO(1)+O(n)$

![:newline 1]
- *Amortized* time complexity for one operation:
$$$\frac{nO(1)+O(n)}{n+1}=O(1)$$$

???

- Best case is the norm
- Worst case happens infrequently

---

## Shrinking strategy

- Halve the array when array is *one-half* full?

![:newline 1]

### Problem
Too expensive for (possible) worst-case scenario:
- Push-pop-push-... sequence when array is full
- Each operation takes linear time

![:scale 100%](images/list_dynamic_array_shrinking.svg)

---

## Shrinking strategy

- Halve the array when array is **one-quarter** full

```C
  void Remove(const size_t pos) {
...
    // Shrink by 2 when reaching 25% of capacity
    if (cur_size <= capacity / 4)
      Resize(capacity / 2);
  }

```

![:filename](list_dynamic_array.h)

]

---

## Conclusion

Pros and cons?

![:newline 1]

### Pros
- Full implementation of the List ADT
- Efficient indexing: $O(1)$
- Efficient insert/remove at end: $O(1)$ *amortized*

???

- Indexing is `Get()`

![:newline 1]

### Cons
- Implementation is more complex
- Some waste of space
    - Array is always between 25% and 100% full
- Inefficient insert/remove at beginning/middle: $O(N)$

---

---

## Fixed array implementation
.lcol55[
.tiny[

```C
template <typename T>
class ListFixedArray {
 private:
  // Fixed capacity of 3 items
  static constexpr size_t capacity = 3;
  std::array<T, capacity> items;
  size_t cur_size = 0;

...
};

```

![:filename](list_fixed_array.h)

]
]
.rcol45[
### Pros and cons
.small[
- (+) Simple implementation
- (-) No flexibility, doesn't fully implement the List API
]
]

![:flush 1]

## Dynamic array implementation
.lcol60[
.tiny[

```C
template <typename T>
class ListDynamicArray {
 private:
  // Initial capacity of 3 items
  size_t capacity = 3;
  std::unique_ptr<T[]> items;
  size_t cur_size = 0;

// Resize array according to new capacity
  void Resize(size_t new_cap) {
    assert(new_cap && new_cap >= cur_size);

```

![:filename](list_dynamic_array.h)

]
]
.rcol40[
### Pros and cons
.small[
- (+) Efficient indexing ($O(1)$)
- (+) Efficient operations at end ($O(1)$ *amortized*)
![:newline]
- (-) Inefficient operations at beginning/middle ($O(N)$)
- (-) Possible waste of space
]
]

---

# Linked list

[![:scale 100%](images/saulgoodman.jpeg)](https://www.youtube.com/watch?v=KqTVkUxMUi8)

![:scale 50%](images/list_singly_ll_insert_3.svg)
---

# Singly linked list implementation

---

???

- Head of the list points on NULL, list is empty

--
![:flush 1]

???

- Insert first value
    - Head points on node containing this value
    - Node has the value, next pointer to NULL

--
![:flush 1]

???

- Insertion at end of the list
    - Nodes points onto new node
    - Node has the value, next pointer to NULL

--
![:flush 1]

???

- Insertion at front of the list
    - Head points onto new node
    - Node has the value, next pointer to previous first node

--
![:flush 1]

???

- Removal middle
    - Rewire next pointer to bypass deleted node
    - Remove node's memory

---

## Data structure

.lcol60.footnotesize[

```C
template <typename T>
class ListSinglyLinked {
 private:
  struct Node {
    T item;
    std::unique_ptr<Node> next;
  };
  std::unique_ptr<Node> head = nullptr;
  size_t cur_size = 0;
...
 public:
  ListSinglyLinked() = default;
...
  ~ListSinglyLinked() = default;
...
};

```

![:filename](list_singly_linked.h)

]
.rcol40[
- Internal node structure: data and next pointer
- Use of smart pointers for ensuring sole ownership
]

???

- Domino effect when list gets destroyed. `head` causes first node to be
  destroyed, `next` of the first node causes second node to be destroyed, and
  so on.

.lcol60.footnotesize[

```C
  Node* GetNode(size_t pos) {
    assert(pos < cur_size);

Node *n = head.get();
    while (pos--)
      n = n->next.get();
    return n;
  }

```

![:filename](list_singly_linked.h)

]

.rcol40[
- Internal `get()` method for access to any node in linked list
    - Use of regular pointer because list traversal is not about ownership
]

???

- What's the complexity of `GetNode()`?

---

## List API (1/3)

```C
  size_t Size() {
    return cur_size;
  }

```

![:filename](list_singly_linked.h)

]

```C
  const T& Get(const size_t pos) {
    if (pos >= cur_size)
      throw std::out_of_range("Position out of range!");

auto n = GetNode(pos);
    return n->item;
  }

```

![:filename](list_singly_linked.h)

]

```C
  int Find(const T &item) {
    int i = 0;
    for (auto n = head.get(); n; n = n->next.get(), i++)
      if (n->item == item)
        return i;
    return -1;
  }

```

![:filename](list_singly_linked.h)

]

???

- Live quiz for complexities!

---

## List API (2/3)

```C
  void Remove(const size_t pos) {
    if (pos >= cur_size)
      throw std::out_of_range("Position out of range!");

if (!pos) {
      // Remove from top of list
      auto n = std::move(head);
      head = std::move(n->next);
    } else {
      // Remove after existing item(s)
      auto prev = GetNode(pos - 1);
      auto n = std::move(prev->next);
      prev->next = std::move(n->next);
    }
    cur_size--;
  }

```

![:filename](list_singly_linked.h)

]

.small[
- Transfer node's ownership to local smart pointer variable `n` with
  `std::move()`
    - Automatically destroyed when goes out of scope

![:newline 0.5]

- Because singly linked list, need to get hold of previous node to remove
  specified node *(not the case with doubly linked lists)*

---

## List API (3/3)

```C
  void Insert(const T &item, const size_t pos) {
    if (pos > cur_size)
      throw std::out_of_range("Position out of range!");

auto n = std::unique_ptr<Node>(new Node);
    n->item = item;

if (pos == 0) {
      // Insert in front
      n->next = std::move(head);
      head = std::move(n);
    } else {
      // Insert after existing item(s)
      auto prev = GetNode(pos - 1);
      n->next = std::move(prev->next);
      prev->next = std::move(n);
    }

cur_size++;
  }

```

![:filename](list_singly_linked.h)

]

.small[
- Usual singly linked list insertion
    - Change head pointer for insertion at beginning
    - Change previous node for insertion at middle or end
]

---

## Conclusion

Pros and cons?

![:newline 1]

### Pros
- Fairly simple implementation
- Insert/remove at beginning: $O(1)$

![:newline 1]

### Cons
- Inefficient indexing: $O(N)$
- Inefficient insert/remove at middle/end: $O(N)$
- Only forward traversal
    * E.g., what would be the complexity of potential API function
      `reverseFind()`?

???

- Live quiz on reverseFind

---

# Doubly linked list implementation

---

## Pointer to previous node

- Efficient reverse traversal
- Easier removal of a node
![:newline 1]

![:scale 70%](images/list_doubly_ll_1.svg)

![:newline 2]

## Optimization: pointer to tail

- Efficient insert/remove at end
- *(Can also be used in singly linked list implementation)*
![:newline 1]

![:scale 60%](images/list_doubly_ll_2.svg)

---

## Conclusion

Pros and cons?

![:newline 1]

### Pros
- Efficient insert/remove at end: $O(1)$
- Possibility of reverse traversal if required by API

![:newline 1]

### Cons:
- Slightly more complex than singly linked list for insertion

---

# Comparison of data structures .ref[\*]

![:newline 2]

.footnotesize[
| Operation                  | Fixed array | Dynamic array      | Linked list                  |
|----------------------------|-------------|--------------------|------------------------------|
| Random access              | $O(1)$      | $O(1)$             | $O(N)$                       |
| Insert/Remove at beginning | N/A         | $O(N)$             | $O(1)$                       |
| Insert/Remove at end       | N/A         | $O(1)$ *amortized* | $O(1)$ (with *tail* pointer) |
| Insert/Remove at middle    | N/A         | $O(N)$             | $search time + O(1)$         |
| Wasted space               | $O(1)$      | $O(N)$             | $O(N)$                       |
]

.footnote[.ref[\*] Big-O only indicates how performance degrades as $N$
increases;  
actual comparison between data structures can also depend on other factors...
(stay tuned)]

---

# Standard C++ containers

---

The C++ Standard Library defines two **popular** implementations of the list ADT
(a.k.a. *sequence containers*):
.lcol75[
- `std::vector`
    - Internally based on a dynamic array
    - *"Unless you have a solid reason not to, use a vector" (Stroustrup, 2013)*
]
.rcol25[
![:scale 100%](images/std_vector.svg)
]
.lcol75[
- `std::list`
    - Internally based on a doubly linked list
]
.rcol25[
![:scale 100%](images/std_list.svg)
]

![:flush 1]

And two other **less popular** implementations:
.lcol75[
- `std::forward_list`
    - Internally based on a singly linked list
    - (Good for empty and very short sequences)
]
.rcol25[
![:scale 100%](images/std_forward_list.svg)
]
.lcol75[
- `std::deque`
    - Double-ended queue
    - Internally based on an array of fixed-size arrays
    - (Good at growing in both directions)
]
.rcol25[
![:scale 100%](images/std_deque.svg)
]

???

- forward_list: surprisingly many uses for empty or short sequences (eg list all
  lastnames of class students by first letter)
    * In WQ25, no last names starting with E, O, Q, R, U, W
- "deque" is pronounced "deck"

---

## Vector

.lcol75.footnotesize[

```C
#include <iostream>
#include <vector>

int main() {
  std::vector<int> v = {7, 5, 16, 8};

// Direct [] access to values
  v[1] = 10;

// Insert at beginning and middle
  v.insert(v.begin(), 42);
  v.insert(v.begin() + v.size() / 2, 23);

// Insert at end
  v.push_back(25);
  v.push_back(13);

// Remove last element
  v.pop_back();

// Iterate and print values
  for (auto n : v)
    std::cout << n << std::endl;

return 0;
}

```

![:filename](std_vector_example.cc)

]

.rcol25.small[
Execution:
```terminal
42
7
23
10
16
8
25
```
]

---

## List

.lcol75.footnotesize[

```C
#include <algorithm>
#include <iostream>
#include <list>

int main() {
  std::list<int> l = { 7, 5, 16, 8 };

// Add an integer to the front of the list
  l.push_front(25);
  // Add an integer to the back of the list
  l.push_back(13);

// Insert an integer before 16 by searching
  auto it = std::find(l.begin(), l.end(), 16);
  if (it != l.end()) {
    l.insert(it, 42);
  }

// Iterate and print values of the list
  for (auto n : l) {
    std::cout << n << std::endl;
  }
}

```

![:filename](std_list_example.cc)

]

.rcol25.small[
Execution:
```terminal
25
7
5
42
16
8
13
```
]

---

.lcol[
## Vector vs List
- Insertion of random integers in collection
- Keep collection sorted
    1. Find proper location
    1. Insert new integer

![:newline 0.5]
- Based on complexity analysis, which container should perform better?
]

???

- Find proper location
    * O(N) for both containers
- Insert value at location
    * O(1) for list
    * O(N) for vector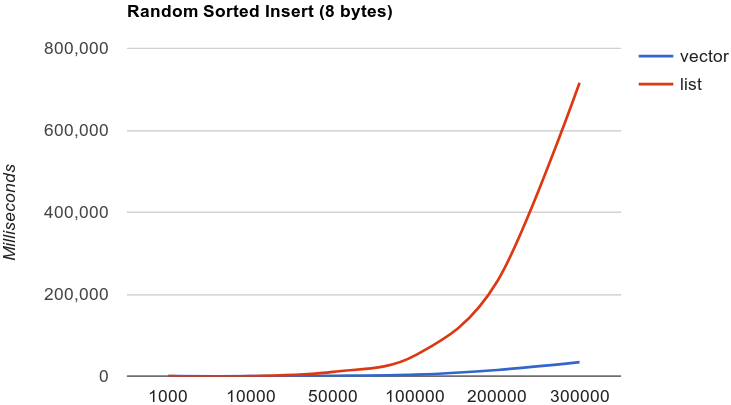

![:flush 1]
.small[
### Explanation
- `std::vector`'s internal array is stored contiguously in memory
    - Much of the array can be cached in processor resulting in very fast access
- `std::list`'s nodes are typically not contiguous in memory
    - Causes lots of physical transfer between processor and RAM memory

### Conclusion
- `std::vector` is generally faster and more efficient than `std::list` *(except
  when dealing with big items)*.ref[\*]
]

.footnote[.ref[\*] More benchmarks:
<https://baptiste-wicht.com/posts/2012/11/cpp-benchmark-vector-vs-list.html>]