Stacks and queues

# CS 10C - Stacks and queues

![:newline]

.Huge[*Prof. Ty Feng*]

![:newline]

.Large[UC Riverside - WQ 2026]

![:newline 6]

![:scale 40%](../utils/style/ucr_cs_logo.png)

???

- Today, self-contained lecture about stacks and queues
- The reason they're not a big topic, is that they're both variations of the
  list ADT which we've already studied in length

---

# The stack ADT

---

## Definition

Subset of a list with two main operations
- **Push**: adds an item to the list
- **Pop**: removes the **most recently** added item from the list

![:newline 1]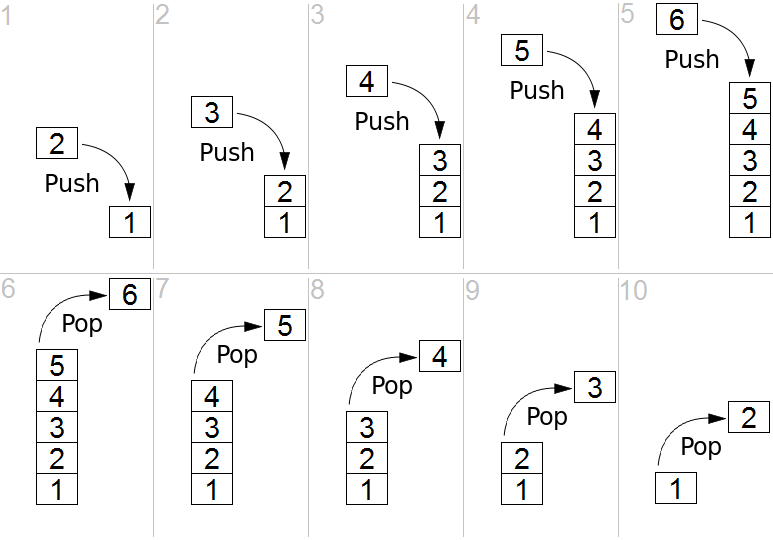

![:scale 60%](images/stack.png)

![:newline 1]
- Also sometimes called **LIFO** (Last In, First Out)

???

- Subset of List
	- But no Get(), Find(), Insert() or Remove()
- Same principle as pile of plates in your cupboard

---

## Typical API

```C
  // Return number of items in stack
  size_t Size();
  // Return top of stack
  T& Top();
  // Remove top of stack
  void Pop();
  // Push item to top of stack
  void Push(const T &item);

```

![:filename](stack_vector.h)

???

- Notice capitalization of first word
    - Google style
![:newline 1]
- Notice the difference between top() and pop()
    - Same as stack in C++ standard library
    - Sometimes, you can have a TopPop() method
![:newline 1]
- Also IsEmpty()?
![:newline 1]
- Have them guess complexity of vector implementation
- list implementation
    - tail pointer and push back
    - or push front

![:newline 1]

- Array (vector)
    - Push and pop to/from *end* of array  
    $O(1)$ *amortized*
]
.rcol33[
![:newline 1]
![:scale 90%](images/stack_vector.svg)
]
![:flush 0]
.lcol66[
- (Singly) linked list
    - Push and pop to/from *beginning* of list  
    $O(1)$
]
.rcol33[
![:scale 100%](images/stack_list.svg)
]

---

## Array implementation

.lcol40.footnotesize[

```C
template <typename T>
class Stack {
...
 private:
  std::vector<T> items;
};

template <typename T>
size_t Stack<T>::Size() {
  return items.size();
}

```

![:filename](stack_vector.h)

]

.rcol60.footnotesize[

```C
template <typename T>
T& Stack<T>::Top() {
  if (!items.size())
    throw std::underflow_error("Empty stack!");
  return items.back();
}

template <typename T>
void Stack<T>::Pop() {
  if (!items.size())
    throw std::underflow_error("Empty stack!");
  items.pop_back();
}

template <typename T>
void Stack<T>::Push(const T &item) {
  items.push_back(item);
}

```

![:filename](stack_vector.h)

]

![:flush 2]
- Entirely based on `std::vector`
    - Wrappers to subset of methods
    - With a bit of error management

???

- By default, `std::vector` doesn't have error management (eg back() on an empty
  vector is undefined behavior)

---

## Linked list implementation

.lcol40.footnotesize[

```C
template <typename T>
class Stack {
...
 private:
  size_t cur_size = 0;
  std::forward_list<T> items;
};

template <typename T>
size_t Stack<T>::Size() {
  return cur_size;
}

```

![:filename](stack_list.h)

]

.rcol60.footnotesize[

```C
template <typename T>
T& Stack<T>::Top() {
  if (!cur_size)
    throw std::underflow_error("Empty stack!");
  return items.front();
}

template <typename T>
void Stack<T>::Pop() {
  if (!cur_size)
    throw std::underflow_error("Empty stack!");
  items.pop_front();
  cur_size--;
}

template <typename T>
void Stack<T>::Push(const T &item) {
  items.push_front(item);
  cur_size++;
}

```

![:filename](stack_list.h)

]

![:flush 2]
- Entirely based on `std::forward_list`
    - With current size info
    - With a bit of error management

???

- Weirdly enough, the forward_list doesn't have a size() method!
    - Implement manually

---

## Some application examples

### Balanced symbol checking

.small[
- Compiler checks that every *right* brace, bracket and parenthesis correspond
  to its *left* counterpart.

```C
    if (array[0) { std::cout << "Hurray!" << std::endl; }
               ^
               error: expected ']' before ')' token
    ```
]

do
        get next token in file
        if token is opening symbol
            push on stack
        else if token is closing symbol
            pop from stack
            if popped symbol is not the corresponding opening symbol
                `report error!`
    while not end of file

if stack not empty
        `report error!`
    ```
]

???

- Same principle for HTML or XML tags

---

### Postfix expressions

- Infix expressions can be interpreted differently, according to which
  precedence is given to operator. Ex: how to calculate `4 + 5 + 6 * 2`?

--
    - Is it `(4 + 5 + 6) * 2 = 30` or `4 + 5 + (6 * 2) = 21`?
    - The latter is the *scientific* answer, as multiply has higher precedence

--
- With a postfix notation (a.k.a. *Reverse Polish Notation*), the order of
  evaluation becomes explicit and does not require parentheses
    - `4 5 + 6 + 2 *` vs `4 5 + 6 2 * +`
    - Used by HP in all their calculators in the 70s and 80s
    - Can easily be computed using a stack!

.lcol.small[
```bash
create empty stack
do
    if token is number then
        push to stack
    else if token is operator then
        pop two numbers from stack
        perform operation
        push result to stack
while there are still tokens

pop final result from stack
```
]

???

- Draw in right column the stack

---

### Postfix evaluation: worked example

Evaluate the postfix expression: `4 5 + 6 2 * +`

.small[
| Token | Action | Stack Contents | Explanation |
|:------|:-------|:---------------|:------------|
| `4`   | Push   | `[4]`          | Operand: push to stack |
| `5`   | Push   | `[4, 5]`       | Operand: push to stack |
| `+`   | Pop, compute, push | `[9]` | Operator: pop 5 and 4, compute 4+5=9, push result |
| `6`   | Push   | `[9, 6]`       | Operand: push to stack |
| `2`   | Push   | `[9, 6, 2]`    | Operand: push to stack |
| `*`   | Pop, compute, push | `[9, 12]` | Operator: pop 2 and 6, compute 6×2=12, push result |
| `+`   | Pop, compute, push | `[21]` | Operator: pop 12 and 9, compute 9+12=21, push result |
]

![:newline 1]

**Final result:** 21 (equivalent to infix: `(4 + 5) + (6 * 2)`)

???

- Walk through this step by step
- Emphasize LIFO property: most recent values are popped first
- Note that for non-commutative operators (-, /), order matters!

---

### Converting infix to postfix

The **Shunting-yard algorithm** (Dijkstra, 1961) converts infix to postfix:

.small[
**Key ideas:**
- Use a stack to hold operators
- Output operands immediately
- Pop operators from stack based on precedence and associativity

**Rules:**
1. If token is operand → output it
2. If token is operator:
   - Pop operators with higher/equal precedence from stack to output
   - Push current operator to stack
3. If token is '(' → push to stack
4. If token is ')' → pop operators until '(' (discard parentheses)
5. At end, pop all remaining operators to output
]

???

- Precedence: * and / before + and -
- Associativity: left-to-right for most operators
- Parentheses override precedence

---

### Infix to postfix: example

Convert `4 + 5 * 6` to postfix:

.small[
| Token | Action | Operator Stack | Output |
|:------|:-------|:---------------|:-------|
| `4`   | Operand → output | `[]` | `4` |
| `+`   | Operator → push (stack empty) | `[+]` | `4` |
| `5`   | Operand → output | `[+]` | `4 5` |
| `*`   | Operator → push (* higher precedence than +) | `[+, *]` | `4 5` |
| `6`   | Operand → output | `[+, *]` | `4 5 6` |
| (end) | Pop all operators | `[]` | `4 5 6 * +` |
]

![:newline 1]

**Result:** `4 5 6 * +` (equivalent to `4 + (5 * 6) = 34`)

???

- Key point: * has higher precedence, so stays on stack
- When we finish, pop everything in order
- This naturally respects operator precedence!

---

### Function calls

- Inherent structure under most function calling conventions
- Call stack:
    - Arguments to a function are pushed into new stackframe
    - Stackframe also holds local variables (e.g. in C)
    - Popped when function returns
    - Supports nested and recursive function calls

void g(void) {
    int a = 4;
    int b = f(a);
}
```
]

???

- What is this function?
    * Factorial

---

### Many other uses

- Java virtual machine
- Undo in word processor
- Back button in web browser
- Etc.

???

- back button
    - stack for back button
    - probably stack for forward button too

---

# The queue ADT

---

## Definition

Also a subset of a list with two main operations:
- **Enqueue**: adds an item to the list
- **Dequeue**: removes the **least recently** added item from the list

![:newline 1]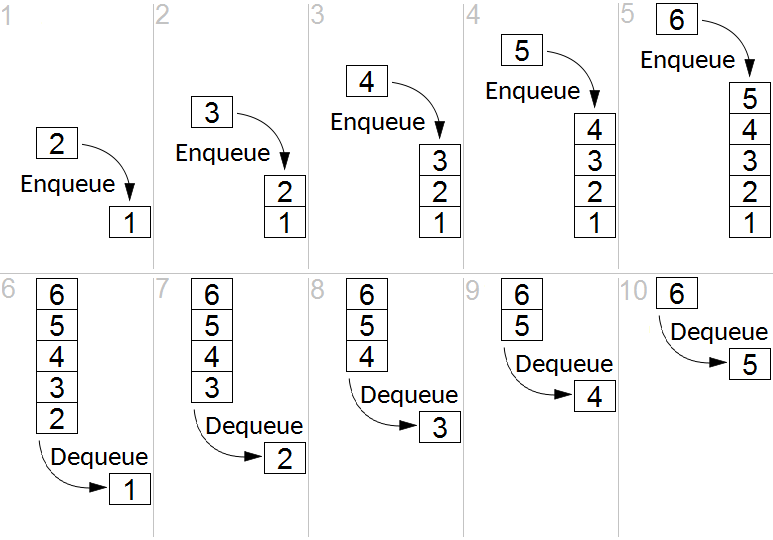

![:scale 60%](images/queue.png)

![:newline 1]

- Also sometimes called **FIFO** (First In, First Out)

???

- Line at any store

---

## Typical API

```C
  // Return number of items in queue
  size_t Size();
  // Return front of queue
  T& Front();
  // Remove front of queue
  void Pop();
  // Push item to back of queue
  void Push(const T &item);

```

![:filename](queue_list.h)

![:newline 1]

## Typical implementations

.lcol66[
- (Doubly) linked list
    - Push to end and pop from beginning of list  
    $O(1)$
]
.rcol33[
![:scale 100%](images/queue_list.svg)
]
![:flush]
.lcol66[
- Circular array
]
.rcol33[
![:scale 100%](images/queue_array.svg)
]

???

- For the list
	- If singly linked list, what's the complexity if push to head, and pop from
	  tail

---

## Linked list implementation

.lcol40.footnotesize[

```C
template <typename T>
class Queue {
...
 private:
  std::list<T> items;
};

template <typename T>
size_t Queue<T>::Size() {
  return items.size();
}

```

![:filename](queue_list.h)

]

.rcol60.footnotesize[

```C
template <typename T>
T& Queue<T>::Front() {
  if (!items.size())
    throw std::underflow_error("Empty queue!");
  return items.front();
}

template <typename T>
void Queue<T>::Pop() {
  if (!items.size())
    throw std::underflow_error("Empty queue!");
  items.pop_front();
}

template <typename T>
void Queue<T>::Push(const T &item) {
  items.push_back(item);
}

```

![:filename](queue_list.h)

]

![:flush 2]
- Entirely based on `std::list`
    - Wrappers to subset of methods
    - With a bit of error management

???

- Note that it could be the exact opposite, there's no consensus on the
  question:
    - enqueue at tail, dequeue at front: => wait line at DMV
    - enqueue at front, dequeue at tail: => food passing through a snake

---

## Some application examples

.lcol[
- Some algorithms related to graphs
]
.rcol[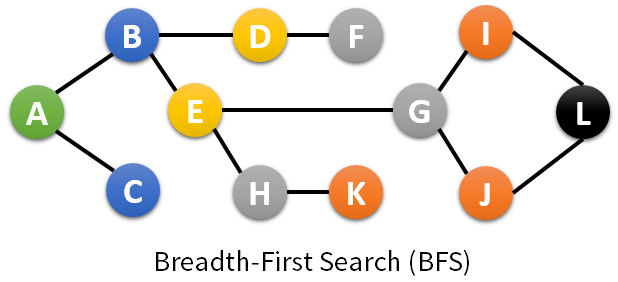
![:scale 50%](images/graph_bfs.png)
]
.wide[
![:newline 0.5]
]
.lcol[
- Queue of jobs for printers
]
.rcol[
![:scale 100%](images/printer_queue.png)
]
.wide[
![:newline 0.5]
]
.lcol[
- Pipes (inter-process communication)
]
.rcol.footnotesize[
```terminal
$ cat final_grades.csv | grep 'F' | wc -l
0
$ echo "Hurray" | banner
...
```
]
.wide[
![:newline 0.5]
]
.lcol[
- I/O requests scheduling (e.g. disk, network)
]
.rcol[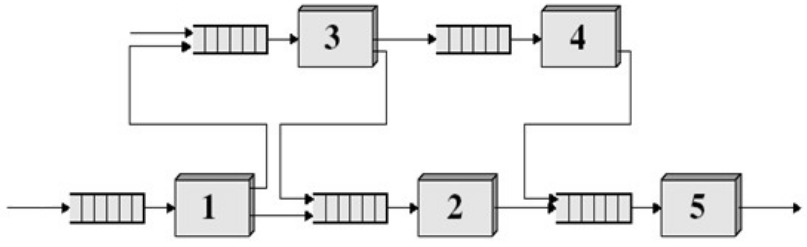
![:scale 100%](images/io_reqs.png)
]

---

# Standard C++ containers

---

The C++ Standard Library defines the implementations of a stack ADT and a queue
ADT.

Both are only *adaptor containers* as they are only wrappers to underlying
sequence containers:
- `std::stack`
    - Can be implemented with `std::deque` *(default)*, `std::list` and
      `std::vector`

```C++
	// By default, will be based on a deque
	std::stack<int> st_dq;

// But can also specify another container
	std::stack<int, std::list<int>> st_lst;
	```

- `std::queue`
    - Can be implemented with `std::deque` *(default)* and `std::list`

---

## The deque container

**Double-ended queue** (`std::deque`) is a sequence container that allows efficient
insertion and deletion at both ends.

.small[
**Key characteristics:**
- $O(1)$ insertion and deletion at both front and back
- $O(1)$ random access (like vector)
- No reallocation of elements (unlike vector)
- Can serve as underlying container for both stack and queue

**Benefits of deque**
- Combines advantages of vector (random access) and list (efficient insertion at both ends)
- More memory efficient than list (no per-element overhead)
- Better cache locality than list, but slightly worse cache locality than vector
]

![:scale 40%](images/std_deque.svg)

???

- Deque = "deck", not "de-queue"
- Best of both worlds for many applications
- Default choice for stack and queue in C++ STL

---

## Deque vs. Vector vs. List

.small[
| Operation | `std::vector` | `std::list` | `std::deque` |
|:----------|:--------------|:------------|:-------------|
| Random access | $O(1)$ | $O(n)$ | $O(1)$ |
| Insert/delete at front | $O(n)$ | $O(1)$ | $O(1)$ |
| Insert/delete at back | $O(1)$ amortized | $O(1)$ | $O(1)$ |
| Insert/delete in middle | $O(n)$ | $SearchTime + O(1)$ | $O(n)$ |
]

- Vector: contiguous memory, good cache locality
- List: non-contiguous, pointer overhead
- Deque: good compromise between the two

---

## Stack

.lcol75.footnotesize[

```C
void check_balance(std::string &str) {
  static const std::string symbols[] = { "({[", ")}]" };
  std::stack<char> balance;

for (auto c : str) {
    // 1. Check if c is an opening symbol
    if (symbols[0].find(c) != std::string::npos) {
      balance.push(c);
      continue;
    }
    // 2. Check if c is an closing symbol
    auto pos = symbols[1].find(c);
    if (pos == std::string::npos)
      continue;  // skip if not

// 3. Check proper symbol matching
    if (!balance.empty() && balance.top() == symbols[0][pos]) {
      balance.pop();
    } else {
      std::cerr << "Unbalanced string!" << std::endl;
      return;
    }
  }

if (!balance.empty())
    std::cerr << "Unbalanced string!" << std::endl;
}

```

![:filename](std_stack_example.cc)

]

.rcol25.small[
Execution:
```terminal
$ "[(){}]"
$ ")"
Unbalanced string!
$ "[(){]"
Unbalanced string!
```
]